Flood risk management research consortium 2 - FRMRC2 (2008-2011)

Funding bodies: Engineering and Physical Science Research Council (EPSRC) under Grant EP/FO20511/1,  EA/Defra (Joint Defra/EA Flood and Coastal Erosion Management R&D Programme), the Northern Ireland Rivers Agency (DARDNI) and Office of Public Works (OPW), Dublin.

This interdisciplinary research Consortium focuses on some of the more recently identified strategic research investigating the prediction and management of flood risk and is the primary UK academic response to this challenge. It is the 2nd phase of the Flood Risk Management Research Consortium (FRMRC), the 1st phase of which was originally launched in February 2004. The concept lying behind this innovative joint funding arrangement is that it allows the Consortium to combine the strengths of fundamental and near-market researchers and research philosophies in a truly multi-disciplinary programme. It has been formulated to address key issues in flood science and engineering and the portfolio of research includes the short-term delivery of tools and techniques to support more accurate flood forecasting and warning, improvements to flood management infrastructure and reduction of flood risk to people, property and the environment. A particular feature of the 2nd phase is the concerted effort to focus on coastal and urban flooding.

The Centre for Water Systems at University of Exeter is involving in the Super Work Package 3 (SWP 3) Urban Flood Modelling, i.e., Work Package (WP) 3.6 On-Line Sewer Flow and Quality Utilising Predictive Modelling and Work Package 3.7 Improved Understanding of the Performance of Local Controls Linking the above and below Ground Components of Urban Flood Flows.

In WP 3.6, the  RAdar Pluvial flooding Identification for Drainage System (RAPIDS) is developed to predict sewer flooding using weather radar information and Artificial Neural Networks.

In WP 3.7, a 3D CFD model is established using OpenFoam software to investigate the flow behaviors via gullies, inlets and manholes. The model is verified and calibrated against the measurements of 1:1 scale laboratory experiment.

ANN techniques

ANNs are well understood and have been extensively reported, so only a brief review is included here for completeness. The fundamental building block is the neuron, which has a number of analogue inputs and one output and implements the transfer function:

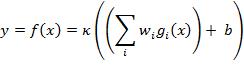
Where: x is the input, gi (x) is some function of x, implemented by the previous neuron towards the input of the network, wi is a weight associated with input i, b is a bias level and ??? is an activation function applied to the output of the neuron. This might typically implement the hyperbolic tangent, a threshold switch or a linear function.

Architectures include fully-connected and layered.  MLP’s generally are layered, but variants with direct connections between the inputs and output layer occur. Feedforward or recurrent designs are possible. Feedforward networks process data unidirectionally from input to output. Recurrent structures allow ANN output at time t to be re-entered into network inputs for computation at time t+1. Next figure illustrates 3-layered feedforward ANN, which is fully-connected within each layer. Note: input layer simply distributes inputs to all neurons in the hidden layer; there are only 2 layers of neurons.

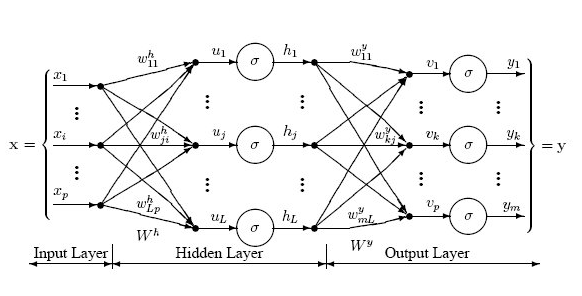
MLPs most commonly use supervised training, in which expected target data are known for a given set of input data. Target data are compared to the output generated by ANN and errors backpropagated towards the input, adjusting weights so as to reduce the output error.   Error optimisation strategies include Scaled-Conjugate-Gradients (SCG) and Quasi-Newton, both of which are gradient-based, aiming to reduce the second-differential of error with respect to weights. AI techniques such as Evolutionary-Algorithms (EA) and Genetic-Algorithms (GA) have been used for ANN training, in which weight space is searched using output correlation with target data set as fitness function.

This study uses supervised training on MLP’s, using a Quasi-Newton or SCG optimisation algorithm.