THE MYTHIC QUEST OF THE HERO: STEPS TOWARDS A SEMIOTIC ANALYSIS OF MATHEMATICAL PROOF

Paul Ernest

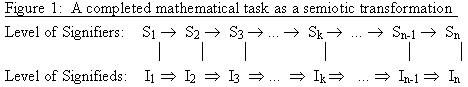
This is a speculative exploration of the semiotics of mathematical text which draws upon diverse sources from philosophy, mythology and literary criticism. It represents an incomplete opening of a line of research, and its tentativity is reflected both in the content and in the adoption of a dialogical style. This allows the counterpoising of different themes without offering a tidy synthesis or end.

Logos

A social constructivist account of proof as a means of persuading the mathematical community is now widely accepted (Ernest 1991, Tymoczko 1986, Hersh 1993). Gaining acceptance from expert judges who act as gatekeepers in mathematics is thus the key epistemological role of proof. But for those who accept that the traditional absolutist role of logic has been dethroned, a question remains. What does the reader of mathematical proof experience that convinces her or him to accept the theorem, instead of flawless logic alone? What psychological processes are involved in the reader experiencing the text? What does the reader of a mathematical proof experience that convinces him or her to accept it? Given that the proof is a text, how does the reader engage with that text decisively?

Mythos

Out of swirling watery chaos, itself the mingling of three god essences, emerged pairs of gods, the second pair Anshar-Kishar giving birth to sky and earth. These were forced apart by wind, creating the frame of the world. In this world, movement personified by the activity of the gods had come into being. The primeval chaos threatens them, but Ea-Enki, the earth, employs a command or spell, a 'word of power' to subdue it. Into the world comes the son of Ea, Marduk (Enlil in earlier versions), the Hero of the creation myth. He collects to himself vast powers, and undertakes a series of adventures, defeating powerful opposing forces, and creates stability and the world order, with the stars in their regular movements.

Logos

This paper offers a tentative social constructivist and semiotic-based exploration of proof, which is intended to also describe the way some learners of mathematics interact with texts and tasks.

First of all every reader of mathematical text or proof approaches the task with a long and complex personal history, and within a socio-cultural context or discursive practice. Every sign, fragment of text, or task in mathematics has two intertwined and inseparable in all but name aspects: that of signifier and signified. My claim is that the realm of signifieds is an imaginary, textually-defined realm, which via processes of intuition ultimately forms the platonic universes that mathematicians' thoughts inhabit. Part of any mathematics learner's or mathematician's role in interpreting a mathematical text is to imagine a miniature math world signified by the text. But in reading a proof or carrying out a classroom task, the reader is following (or accomplishing) the transformation of that text. In doing this, according to Rotman's (1993) analysis the mathematician is carrying out imagined text based actions. In reading a proof, these involve imagined actions coupled with transformations of text which have a cyclic pattern. The beginning is the announcement of the endpoint, the theorem to be proved. This is followed by an imagined voyage through text and underlying math-world, until the endpoint is reached. (For the learner undertaking a mathematical task, the beginning is a pointer to the endpoint – a directive to 'solve' the problem: this is both to undertake a quest, and to transform a text.)

According to Rotman (1993) the mathematician alternates his identity or subjectivity between that of the mathematician and his agent: the imagined skeletal representation of self - like the moving fingertip on a map retracing a journey. This representation of self - like the turtle in Logo - or the hero/agent in a computer adventure game - traces out a journey of adventure, analogous to the universal 'hero with a thousand faces' in Campbell's (1956) mythic cycle.

Mythos

In the beginning was the Word, and the Word was with God, and the Word was God. ... And the Word was made flesh.

In the beginning God created the heaven and the earth.

And the earth was without form, and void; and darkness was upon the face of the deep. And the Spirit of God moved upon the face of the waters.

And God said, Let there be light: and there was light.

And God saw the light, that it was good: and God divided the light from the darkness.

And God said, Let there be a firmament in the midst of the waters, and let it divide the waters from the waters.

And God made the firmament, and divided the waters which were under the firmament from the waters which were above the firmament: and it was so.

Who utters these words? Is it God who is word and utters word? Is it humanity who hears the word and tells the story beginning a never-ending dialogue?

Logos

In the paper I explore this analogy, and also that between algorithm and proof, and argue that the latter pair have more in common than is often acknowledged. Thus involvement in the procedures of school mathematics provides an apprenticeship for the future mathematician, in which she learns to project her self into the script, programme, or imagined math-world of the mathematical task. However my conjecture is that the future mathematician learns (1) to obey the imperatives in mathematical text, (2) to write such mathematical texts, and (3) to jump out of the script (i.e. change role from subjected agent to mathematician) and critique it. However many others learn only to be a regulated subject (i.e.1 above), carrying out on paper and in mind what it needs only a machine to do.

Mythos

In the beginning there is a primal Unity, a state of indistinction or fusion in which factors that will later become distinct are merged together.

Out of this Unity emerge, by separation, pairs of opposite things or 'powers'...This separating out finally leads to...the world-order and the formation of the heavenly bodies

The opposites interact or reunite, in...phenomena and in the production of individual...things.

Logos

It has been remarked that in modern Anglo-Saxon thought there are two incommensurate cultures, that of science and that of the humanities and literary thought (Snow 1959).

However much modern continental European philosophy and post-modernist thought reject this division and parallel dichotomies such as the following: absolute logical knowledge versus fallible empirical knowledge, representational language versus poetic language, mind and rational thought versus body and feeling, word versus deed, Logos versus Mythos.

What has emerged from such perspectives is the pre-eminence of language and narrative, concretely realised in the world. According to Lyotard (1979) all scientific knowledge must present itself as a narrative to legitimate itself.

No one doubts that literature, philosophy, and mathematics once had "primitive" connections. ... [T]heir more contemporary objects and "objectivities" are, like all that seems prime, no less compellingly entwined. (Smyth 1995, 648)

Mythos

Out of the chaos of informal human and mathematical conversation, experience and knowledge comes the linguistic sign. This bifurcates into the signifier and the signified. The sign brings into existence the Assumed and the Unassumed, the Expressed and the Unexpressed, the Belonging and the Excluded, the True and the False. Out of the Assumed, the Expressed and the Belonging is formed the math-world. In it emerges the Subject (or Agent) with powers defined by the math-world, who starts to construct the world order. Thus a theory, especially a foundational theory, is constructed in a mathematical creation myth.

In this way, Euclid's Elements begins with a pregnant void, into which is defined a point, with no parts or magnitude, the centre and location of the subject in geometry. The point multiplies, and Line is brought into existence, followed by Plane, Angle, and Plane Figures. All of these exist at first only as Ideal Types, in the textual space of definitions, not yet born in the math-world of Euclidean Space. The postulates specify the power of an Agent; to draw lines and circles in the math-world. The axioms specify the power of the Subject in making textual transformations; which icons and signs may be transformed into others (the properties of identity). Other postulates and axioms describe the intended structural and textual constraints (the rules) of Geometry, such as the uniqueness of right angles and parallel lines, and how set inclusion implies corresponding measure order relations.

Logos

From such a perspective, all mathematical and scientific knowledge, mathematical proof in particular, are discursive forms, are narratives. Thus it is appropriate to apply the tools of linguistics, semiotics and literary analysis to mathematics. Thus I pose the questions: What tales do mathematical proof narratives tell? Who is the teller of mathematical tales and who is the listener? What syntactical and linguistic forms are employed in the story and how do they relate to the content of the tale? If mathematics is written in sentences what are their subjects, objects and verbs? How are the ideas of necessity and certainty of mathematical knowledge formed and expressed? How is the platonic realm of mathematical forms and objects created and sustained by mathematical narratives?

Mythos

Thus the scene is set for the construction of Euclidean geometry, the math and textual worlds created, awaiting the adventures of the Hero, and the Agent/Subject invisibly in place, with powers of textual transformation and of the construction of mathematical objects in the math-world. Now begins a series of adventures (the propositions). These are textual narratives, with ancillary iconic illustrations (maps of the math-world), in which the Agent uses its powers to construct increasingly elaborate figures, and textual transformations describe necessary properties of the constructed figures. The outcome is both a persuasive narrative, and the development of a new power for the Agent. or of a new legitimate textual transformation. (The persuasive aspect legitimates the new powers of the agent.) The Elements of Euclid, through a sequence of propositions, each itself a linked instance of a hero-cycle, brings into being and elaborates a math-world. It is a creation myth. It tells the story of the creation of the world of Geometry. Indeed, it is the creation of the world of Geometry, for the Storyrealm and the Taleworld it creates are inseparable. For the reader, whose geometric agency runs through the narrative, garnering powers, it creates the subjective math world corresponding to this cultural math world.

Logos

Young (1987) proposes a structured theory of narrative based on the frame analysis of Goffman, Natanson and others. She locates narratives in the realm of conversation, and regards them as existing on two levels, or in two frames. First there is the storyrealm, which is the narrative text itself. Second, there is the Taleworld, the framed world of meanings created, referred to and traversed in the narrative. Each of these realms exists within a frame, which is indicated by opening and closing markers signalling the move in or out of the frame. According to her theory, the following common structure is shared by narratives. Within the realm of conversation, a 'preface' announces a coming narrative, and an 'opening' indicates a move into the storyrealm, where the narrative begins. Following this a 'beginning' indicates a shift into the Taleworld, where the story unfolds until it reaches its conclusion or 'end'. This signals a move back out of Taleworld into the storyrealm. A further move out of the storyrealm is signalled or framed by a 'closing', and back in the realm of conversation a 'coda' puts a final marker to show that the storyrealm is closed.

This structure suggests both a symmetry and a cyclic structure to narratives, which begin and end with a single narrator in the realm of conversation. From this start, they move into the Taleworld, cross the threshold into the storyrealm, traverse the tale itself, then cross back into storyrealm, and before finally returning into the realm of conversation. There is a strong symmetry (reflectional symmetry in time) with matched openings and closings throughout. This symmetry, with the consequent return to the original realm of conversation, gives the structure an implicit circularity.

This theoretical account suits that of mathematical proof well in several ways. A semi-formal or informal proof is a narrative, which begins at the level of language (the signifier level), moves to that of meanings (the level of signifieds), and then finally returns to the level of language at the end. It is also a cyclic narrative, as I shall further elaborate below. There are markers in proofs indicating openings or beginnings and closings or ends. Thus there is a good fit between the patterns. One are of difference is that a semiformal proof may alternate between the level of language and that of meanings more than once, unlike the story pattern. But that could easily be generalized; and indeed modern novels and film narratives often alternate between the levels of medium and content several times.

A mathematical proof or problem-solving task in mathematics (see Ernest 1993) may thus be seen to have a similar structure, comprising a sequence of signs which can be understood both as a sequence of textual transformations on the level of signifiers (the storyrealm) and of conceptual transformations on the level of signifieds (the Taleworld).

A simplified diagram illustrating these transformations is shown in Figure 1.

Figure 1: A completed mathematical task as a semiotic transformation

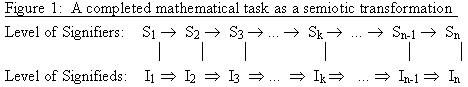
I shall leave aside tasks and focus on proof here. In mathematical terms, this transformational 'narrative' can be understood as have a cyclic structure because it begins with the statement of theorem to be proved, and ends by returning to the theorem, but this time having reached it with a proof, having provided an epistemological warrant for it. Mathematically, we can understand a mathematical proof as having the following structure

The Cyclic Pattern of Mathematical Proof

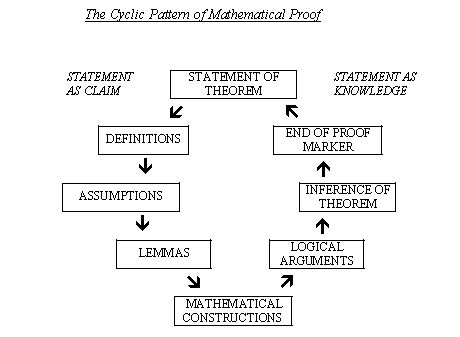
The stages in the journey are:
Statement of theorem,
Assumptions,
Definitions,
Lemmas,
Mathematical constructions
'Logical' arguments,
Inference of theorem
End marker (Halmos bar)

Mythos

Like the Creation Myth of Genesis, that of Euclid is an ur-myth for Western Culture. It brings into being a world and an Agent, and then charts the further construction and elaboration of that world by the Agent's powers. The foundationist narratives of Logicism, intuitionism, and indeed the account of many formal mathematical theories follows the Creation Myth pattern.

Brouwer's Intuitionism provides an idealistic account of the creation of mathematics in the mind of the Mathematician. There mathematics emerges from, out of the chaos of phenomenological experience. (Like Berkeley's epistemology, it assumes that knowing is grounded in an omniscient consciousness, or at least a universal consciousness). It begins with the awareness of

the falling apart of moments of life into qualitatively different parts, to be reunited only while remaining separated by time, as the fundamental phenomenon of the human intellect, passing by abstracting from its emotional content into the fundamental phenomenon of mathematical thinking, the intuition of the bare two-oneness. This intuition of two-oneness, the basal intuition of mathematics, creates not only the numbers one and two, but also all finite ordinal numbers, inasmuch as one of the elements of the two-oneness may be thought of as a new two-oneness, which process may be repeated indefinitely; this gives rise still further to the smallest infinite ordinal number . Finally, this basal intuition of mathematics, in which the connected and the separate, the continuous and the discrete are united, gives rise immediately to the intuition of the linear continuum, i.e., of the 'between,' which is not two-oneness. (Brouwer 1913, 69)

Here the Math-world is a recess or niche in he phenomenological world of the Mathematician (not too dissimilar from Berkeley's account of existents as percepts in the mind of God). Within that global space, an agency is projected downwards to become the Constructive Agent, whose limited powers, through various adventures and Hero Cycles, lead to the construction of Intuitionist Mathematics. One of the unique features of Intuitionism is the concern with the precise powers of the Agent. These are not extended and idealised beyond those of a mathematician as far as those of the Agent in classical mathematics. Intuitionism and constructivism in general are concerned to allow just those powers to the agent which seem appropriate, according to some, varying conception of what journeys can be undertaken in Math-world. This links to the view that intuitionistic mathematics should in some way be the pre-linguistic adventures of the Agent/Hero, although I reject this perspective of it. Classical mathematics admits a range of transformations which can be applied to signifiers themselves, and does not focus exclusively on the domain of signifiers. Indeed it all the while seeks to minimise reliance on the realm of signifieds.

Logos

Johnson (1987) argues that many of our most abstract ideas originate in a range of basic bodily experiences and experiential conceptions. He suggests that the presence of such conceptions is revealed through the pattern of metaphors we use in texts and conversation. In particular, he points to the centrality of the metaphors of path and journey for logical reasoning or deduction.

Let us begin with the way we understand formal reasoning. When we reason, we understand ourselves starting at some point (a proposition or set of premises) from which we proceed in a series of steps to a conclusion (a goal, or stopping point). Metaphorically, we understand the process of reasoning as a form of motion along a path--propositions are the locations (or bounded areas) that we start out from, proceed through, and wind up at. Holding a proposition is understood metaphorically as being located at that point (or in that area). This very general metaphorical system is reflected in our language about reasoning in a large number of ways. (Johnson 1987: 38)

Descriptions of proof include figures of speech reflecting this underlying metaphor. A proof has a "starting point", followed by "proof steps" "to reach" the "intended endpoint". Thus a proof can be interpreted as a cyclical journey. My claim is that this is part of a deep and shared meaning of all proof structures.

In modern English uses the term 'premises' is used both for the assumptions of a proof, and for a house, which is presumably the starting point of most journeys. This fits well with the metaphor of proof as journey. Etymologically, this double meaning of 'premises' does not arise from the metaphor. Historically the disposition of property in legal conveyancing was contained in the early section, the 'premises of the deed'. Through a metonymic shift, the term premises has become the general name of a building.

Mythos

Homage to thee, Osiris, Lord of eternity, King of the Gods, whose names are manifold. ... Thou art the Lord to whom praises are ascribed in the name of Ati.

Thy name is established in the mouths of men. Thou art the substance of Two Lands. Thou art Tem, the feeder of Kau (Doubles)

Thy fear is set in all the lands by reason of thy perfect love, and they cry out to thy name making it the first of names.

Logos

It needs to be made clear that the transformational narrative which is a proof need not consist of a straightforward transformation. While Lakatos' informal thought experiment proof is likely to be of this type, as is illustrated in the earlier proofs of the Euler Relation (Lakatos, 1976), more formal proofs can be rather more convoluted. They may, for example, assume the opposite of the theorem to be proved, and then proceed by the method of proof by contradiction. Although this particular form, proof by contradiction, is controversial to the extent that it is rejected by constructivists, Intuitionists, in particular, because it does not allow the theorem to be directly constructed.

Mythos

The pattern of proof finds a full analogue in the Hero Cycle proposed by Campbell (1956) in his analysis of ancient religious and cultural myths. In this cycle the mythological hero leaves his familiar surroundings, sets off on his quest, and having accomplished it, returns, transformed or enriched in the process.

The standard path of the mythological adventure of the hero is a magnification of the formula represented in the rites of passage: separation--initiation--return: which might be named the nuclear unit of the monomyth. A hero ventures forth from the world of common day into a region of supernatural wonder: fabulous forces are encountered and a decisive victory is won: the hero comes back from this mysterious adventure with the power to bestow boons on his fellow [hu]man[s]. Campbell (1956: 30)

In elaborating on this cycle Campbell remarks on a number of key stages. It begins with the hero hearing an announcement or call to adventure. The hero meets a helper, and then crosses the threshold into the realm of adventure. There he may meet and pass certain tests, and be aided by further helpers or tools. He then accomplishes the central task or object of the adventure. This is followed by the return, possibly in flight, bearing the powers, gift, knowledge or elixir. The hero then re-crosses the threshold out of the realm of adventure into the starting realm. He returns to his starting point enhanced by his newly gift, and the cycle is complete.

This is typified in the archetypal quest narrative of Homer, the Odyssey, and is the shared pattern of all hero myths, Odysseus, Wotan, the Frog King, the Trickster, Jesus Christ, Finn McCool and Buddha.

Logos

Another analogue of cyclic transformation can be found in Alchemy, in which a common substance following complex (Al)chemical procedures is transformed into gold. Both of these types of narrative of transformation can be understood as allegorical accounts of spiritual enlightenment in which the initiate's mind goes on a voyage of self-discovery and returns, but transformed and elevated to a higher level (Jung, 1974). In other words, the cycle results in the acquisition of knowledge.

The features of the hero cycle resemble the story and myth analysis of the Russian formalists Propp and Todorov. Propp (1928) notes a shared formal structure and sequence of functions in many myths and folk-tales, which he claims all end in some form of gratified desire or successful quest. In the same way, all proofs seek through transformations to reach their intended and preordained endpoint, the theorem to be proved. Thus a partial analogy between proofs and such structures can be noted. Propp describes archetypal characters who appear in tales as hero, villain, dispatcher, false hero, donor, helper, princess, father. Counterparts of many of these characters occur in Campbell's Hero Cycle. Of course mathematical proofs do not have personal characters. So to press the metaphor I have to use what might be termed the 'reverse allegorical function': converting characters into abstract objects and concepts or expressions. Similarly (but oppositely), in allegories such as Buchan's Pilgrim's Progress, abstract objects concepts or terms are turned by an 'allegorical function' into persons, places and other concrete particulars.

Mythos

What we call the beginning is often the end
And to make an end is to make a beginning.
The end is where we start from.
...
We shall not cease from exploration
And the end of all of our exploring
Will be to arrive where we started
And to know the place for the first time.
Eliot (1944: 42-3)

Logos

The interdependence of ends and beginnings in narratives is stressed by Young.

The appearance of consequentiality in narrative is produced by counting the last event taken from the Taleworld as an end, and then constructing the story backwards to include whatever is necessary to account for it, thus arriving at the beginning. Beginnings do not so much imply ends as ends entail beginnings. Young (1987: 29)

In a mathematical proof, the theorem is first stated as a conjecture, or statement-to-be-proved, and then after a transformational sequence or journey it reappears, justified and enhanced. Furthermore, to achieve the desired endpoint, the journey to it must be constructed with that end in mind. So the end informs the beginning, and all the subsequent stages. Overall, the beginning is indeed the end, and by the end there is new knowledge of the beginning.

There is thus a parallel between Campbell's hero myth cycle and mathematical proof , which can be brought out, using the stages in Young theory of narrative.

The parallel is good in many points, and weak in others. Thus the hero myth cycle could be matched with the tale in the Taleworld, but this would reduce the significance of the threshold crossing, and its parallel with the move from the level of signifiers to the realm of signifieds. The parallel also leaves a number of questions unanswered. Such as, what is a proof about? Beyond its structure, what is its subject matter or subject? Is there an analogue to the hero?

Mythos

Rotman (1993) draws on C. S. Peirce's notion that a proof is a kind of diagram and that in following a proof you are projecting a miniature image of yourself through some kind of terrain. The person can engage with, can read or write an normal text. In contrast the mathematician has a different kind of subjectivity to the person and has to relinquish certain resources a person has - in reading and writing, s/he has no access to indexicals - s/he can't refer to himself, or time or space, the genre that s/he has to engage with is one that is objectified, it has been cleansed of particular reference. The genre of mathematical writing is thus in an eternal present tense. , where if there is an individual pronoun, personal pronoun, it would be `we', which somehow is carrying a mathematical community through, or it could be the writer is carrying the reader through (like Virgil and Dante).

Logos

A mathematician reading mathematics also creates an agent: a mindless, unreflective automaton which is the tiniest identity within the of Chinese box of identities created, and when the text says "let ...", or "we sum this to infinity", it is this little agent who zips off in his imagined space, and carries out these actions. In doing mathematics we learn to create agents, and we are persuaded by the imagined actions of these agents. Rotman argues that proofs are fundamentally claims about what an agent can do under the circumstances laid out, and also series of instructions, or programmes, and the reader has to imagine the agent going through the prescribed actions.

A convincing proof is one in which the constructions, passages, imagined transformations seem to inevitably achieve the required and predicted end result.

Where is the hero? There is nobody in a proof, it is an empty formal structure, so how can there be a hero or any character? The hero is the wave-front of the readers attention as it progresses through the proof. It may be in the form of mathematician, reading the text and imagining the virtual space it signifies. It may be in the form of the agent carrying out the imagined procedures, etc., of the text. There is no hero in the text until the mathematician-reader passes the text through his/her mind, or rather passes his/her mind through the text.

References

Brouwer, L. E. J. (1913) Intuitionism and Formalism, in Benacerraf, P. and Putnam, H. Eds (1964) Philosophy of Mathematics: Selected readings, Englewood Cliffs, New Jersey: Prentice-Hall, 66-77.
Campbell, J. (1956) The Hero with a Thousand Faces, Cleveland: Meridian Books.
Eliot, T. S. (1944) The Four Quartets, London: Faber.
Ernest 1991, Ernest, P. (1991) Philosophy of Mathematics Education, London: Falmer Press.
Ernest, P. (1993) Mathematical Activity and Rhetoric: Towards a Social Constructivist Account, in I. Hirabayashi, N. Nohda, K. Shigematsu, F. L. Lin, Eds, Proceedings of PME-17 Conference, Tsukuba, Japan: University of Tsukuba, Volume 2, 238-245.
Ernest, P. (1994) The dialogical nature of mathematics, in Ernest, P. Ed. Mathematics, Education and Philosophy: An International Perspective, London, The Falmer Press, 1994, 33-48.
Hersh, R. (1993) Proving is Convincing and Explaining, Educational Studies in Mathematics, 24 (4) 389-399.
Jacobsen, T. (1946) Mesopotamia (chapters 5-7), in Frankfurt, H., Frankfurt, H. A., Wilson, J. A. and Jacobsen, T. (1946) Before Philosophy, London: Pelican Books.
Johnson, M. (1987) The Body in the Mind, Chicago: University of Chicago Press.
Jung, C. G. (1974) Dreams (trans. R. F. C. Hull), Princeton, N. J.: Bollingen Series, Princeton University Press.
Lakatos, I. (1976) Proofs and Refutations, Cambridge: Cambridge University Press.
Lyotard, J. F. (1984) The Postmodern Condition: A Report on Knowledge, Manchester: Manchester University Press.
Munitz, M. K. (1957) Theories of the Universe, New York: Free Press.
Propp, V. I. (1928) Morphology of the Folk Tale, (Translation published University of Texas Press, 1958).
Rotman, B. (1993) Ad Infinitum The Ghost in Turing's Machine: Taking God Out of Mathematics and Putting the Body Back in, Stanford California: Stanford University Press.
Smyth, J. V. (1995) A Glance at SunSet, in Smith, B. H. and Plotnitsky, A. Eds Mathematics, Science and Postclassical Theory, Special issue of The South Atlantic Quarterly, 94 (2) 619-654.
Snow, C. P. (1959) The Two Cultures and the Scientific Revolution, Cambridge: Cambridge University Press.
Tymoczko, T. Ed. (1986) New Directions in the Philosophy of Mathematics, Boston: Birkhauser.
Young, K. G. (1987) Taleworlds and Storyrealms, Dordrecht: Martinus Nijhoff.