Lim Chap Sam
School of Educational Studies
Universiti Sains Malaysia
11800 Penang, Malaysia
cslim(at) usm.my
@ is replaced by (at) to stop the automatic garnering of email addresses by Spam factories - Editor
Abstract *
This paper aims to discuss some preliminary findings of two
case studies, which were part of a bigger research project exploring the culture
of m athematics teaching and learning in some Malaysian schools. These two case
studies focus on exploring the characteristics or culture of mathematics learning
in two Chinese primary schools.
The study is interpretative in approach and employs mainly
qualita tive methods for data collection. These methods include planned interviews
with the school administrators, teachers, parents and pupils, videotaped classroom
observations and participant observation of selected school activities that
related to mathematic s teaching and learning.
Preliminary findings of these case studies highlighted the
dominant characteristics of � drills and practices� in these Chinese schools.
This finding concurred with earlier studies (such as Lim & Chan, 1993; Munirah
& Lim, 1996) t hat it might be true that the quantity of exercises and homework
given are comparatively much more than the other types of primary schools, there
are other more important contributing factors. These factors include the quality
of exercises given, the beli e fs and expectation of teachers and parents, the
pupils ’ image of mathematics and mathematics learning, as well as the cultural
values about mathematics education.
Introduction
Being a multi-ethnic and multi-cultural country, Malaysia has a unique educatio nal system whereby there are three types of primary schools available depending upon the medium of instruction. These are: (a) Malay medium national schools (SK); (b) Chinese medium national type schools (SRJKC); and (c) Tamil medium national type schools (SRJKT). Although the medium of instruction is different, all schools follow a national mathematics curriculum, and all pupils sit for a national examination, the Primary School Achievement Test or UPSR at the end of the six years of primary schooling. Fo r the past decades, the results of the Primary national examinations (UPSR) have shown that pupils from the Chinese medium schools perform consistently better in mathematics than those in the other types of schools. Table 1 displays the percentage of passe s of the various types of schools in the UPSR examination.
Table 1: Mathematics Achievement in the UPSR Examination (Percentage of Passes) by Types of Schools
| Year | Type of school | ||||
|---|---|---|---|---|---|
|
SK/SRK (Malay medium) |
SRJKC (Chinese medium) |
SRJKT (Tamil medium) |
|||
| 1991 |
60. 4 |
86.6 |
49.9 |
||
| 1992 |
60.6 |
86.8 |
56.1 |
||
| 1993 |
63.1 |
87.6 |
55.8 |
||
| 1994 |
64.0 |
86.3 |
58.1 |
||
| 1995 |
67.9 |
87.6 |
59.0 |
||
| 1996 |
74.5 |
90.0 |
65.2 |
||
| 1997 |
- |
85.5 |
- |
||
| 1998 |
77.5 |
91.2 |
68.6 |
||
| 1999 |
76.2 |
90.0 |
70.9 |
||
| 2000 |
77.5 |
87.5 |
73.9 |
||
|
2001 |
76.0 |
89.9 |
74.4 |
||
Source: Malaysian Examination Board Yea
rly Report for the year 1991-2001.
Note: SK/SRK = National/National type Primary school
(Malay language as medium of instruction)
SRJKC
= National Type Chinese Primary school (Chinese language as
medium of instruction)
SRJKT = National Type Tamil Primary
school (Tamil language as medium of instruction)
This raises concern especially to mathematics educators and the Ministry of Education. The Ministry of Education has since attempted to upgrade the mathematics achievement of the Malay medium school s. Even the Prime Minister himself has advocated the need for the government school authorities to emulate the commitment of the Chinese schools to education. The Malay medium schools were asked to adopt the teaching approaches of the Chinese medium schoo l . Some ministers even suggest the possibility of 'importing' mathematics teachers from Chinese schools to the Malay schools (The Star, 21 January, 1992). However, this proposal is yet to be tried. Indeed, as shown by Table 1, these attempts seem to have s h own some success as the achievement gap between the various types of schools is narrowing. Nevertheless, this issue is not that simple. Mathematics is neither culture-free nor value-free (Ernest, 1991) but a form of culturally transmitted knowledge (Bisho p , 1988). The success in mathematics learning among these schools may have been related to the school culture and its related community culture. Thus, can culture be "imported" from one school to another, by merely exchanging the mathematics teachers?
There seems
to have an assumption that Chinese medium school pupils perform better in mathematics,
because these schools have some � special recipe� in their teaching and learning
of mathematics. This assumption has stirred up a lot of interest in researching
th e secret of success in Chinese primary schools .
Review of related local literature shows that so far three
studies (Lim & Chan, 1993; Munirah & Lim, 1996; Yong et al., 1997) have
been carried out in Malaysia to compare mathematics learning among the differ
ent cultural groups of Malaysia. Lim and Chan (1993) compare the mathematics
achievement of two groups of Primary Six Malay pupils, one group studied in
SRJKC (Chinese) schools whereas another group studied in SK (Malay) schools.
They also compared the te a ching strategies, learning facilities, and the amount
of exercises given by these two types of schools. Likewise, Munirah and Lim
(1996) compared mathematics teaching and learning between one Chinese primary
school (SRJKC) and one Malay primary school (SK ) which are located in the same
area, by classroom observation and interviews with the headmaster, mathematics
teachers and some pupils of the respective schools. Unlike the above two studies,
Yoong Suan and his colleagues (1997) focus on investigating the acquisition
of basic number concepts among the Malaysian Primary One pupils of different
ethnic and cultural backgrounds.
Although all
the above three studies were exploratory in nature and their findings were far
from conclusive, there were at least two significant issues that can be drawn
out from these studies. First, language seems to play a significant role in
mathematics learning. As pointed out by Yong et al (1997), the Chinese language
seems to have a cultural advantage over the other two language s , Malay and
Tamil, particularly in terms of its simpler and consistent number-naming system.
It follows that any student, be he/she Chinese, Malay or Indian-who is trained
to use this numbering system may be able to count and memorize the number system
fa s ter than his/her counterparts who use other languages. Second, findings
from the above three studies strongly suggest that there are differences in
teaching approaches that are adopted by the different medium schools. Chinese
medium schools seem to favour more � lively learning atmosphere in class� ;
� plenty of drills and practices� ; � more homework� , � more tuition� as well
as � more competition and quizzes� (Munirah & Lim, 1996). Consequently,
pupils of the Chinese medium schools tend to perform better in com p utational
skills and counting of number, as well as memorisation of multiplication tables.
Even Malay pupils studying in Chinese medium schools were found to perform better
than their counterparts in other medium schools with regard to computational
skill s (Lim & Chan,1993).
Yet are the above two factors: language and teaching approaches
(in particular, a lot of drills and practices) sufficient to explain the possible
better achievement of the Chinese medium schools? Drill and practice is often
equate to rote-learning. Rote learning is taken as learning by memorising and
without understanding. Thus, rote learning is not meaningful and often attribute
to students ’ dislike of mathematics. Therefore, how can this dominant culture
of drill and practice contr i bute to the better mathematics achievement of
the Chinese primary schools?
A research project that aims to explore the impact of culture
on mathematics teaching and learning in some Malaysian schools was carried out
in 2001. Here I give a brief descriptio n of the study:
The study
In this study,
culture is defined as � a system of shared knowledge and beliefs that shaped
human perceptions and generates social behaviours� (Bennett, 1990, p.47). It
follows that the culture of mathematics learning is conceptual ised as � a system
of shared knowledge, practices, beliefs and values in mathematics learning�
.
The objectives of the study are:
1) To explore and identify cultural values that are
inherent in the teaching and learning of mathematics in different types of Mal
aysian secondary schools.
2) To explore how these cultural values have been manifested
in practice and how they act as � host� culture for the teaching and learning
of mathematics in these schools.
3) To identify the attributes or qualities of a successful
mathem atics learner in Malaysian schools.
The participants
The study involved
four pairs of schools. Each pair consisted of one secondary school and its main
feeder primary school. These schools were selected in pair to study the continuity
of the cultural infl uences. It is believed that the inculcation of the culture
of learning mathematics begins in primary school and it will be brought into
secondary school. A student ’ s view, beliefs and values of mathematics
learning may change as he or she enters higher fo r m, but the primary mathematics
learning experiences remain influential.
Eight schools, four each from the state of Kedah and Penang
were selected as case studies. Each case study involves the school as a unit
and the community in which it is situated. T he school consists of its members
(tha t includes school administrators, teachers and pupils) while the community
consists of the school board and parents of pupils.
Method
The study is
interpretative in approach and employs mainly qualitative methods for data collection.
These methods include planned interviews with the school administrators, mathematics
teachers, parents and pupils, videotaped classroom observations and participant
observation of s ome school activities that are related to mathematics tea ching
and learning. For example, the researcher s attended and participated in some
schools activities like mathematics department meeting (mesyu a rat panitia
matematik) and motivation camp for additional mathematics . All interviews were
tape-recoded and tra nscribed for qualitative analysis.
However, for the purpose of this paper, only findings of
two case studies on two Chinese primary schools will be discussed.
Findings and discussion
Findings discussed here are drawn on the analysis of 47 interview tran scripts of the various members of the community of the two schools studied, mainly the school administrators, mathematics teachers, parents and pupils. Here I begin with a brief description of the background of the two schools studied, before I highlight s ome characteristics of these schools that may have contributed to their success in mathematics. In particular, the beliefs of drill and practice in learning mathematics. It is interesting to observe that these two schools share more similarities than diff e rences in the culture of mathematics learning.
Case 1: Primary school H
Primary school H is a small school with a total enrolment of only 206 pupils , 12 teachers, a headmistress and 2 supporting staff. The ethnic composition of the pupils is majority Chin ese (about 98% ) . All the mathematics teach ers are Chinese . It is located in the centre of an urban city. The majority of its pupils live nearby and come from middle to lower income families. As the data indicate, out of the 9 parents whom we interviewed, o nly one mother is a housewife; all the others are working parents. Most of them are small entrepreneurs such as stationery shopkeeper, photographer, goldsmith, hairdresser or tailor. The school has achieved 100% passes in UPSR mathematics for the last two years (2000 & 2001).
Case 2: Primary school B
Primary school B has 1400 pupils with 51 teachers, 3 deputy headmasters and one headmaster, as well as 9 supporting staff. The ethnic composition of the pupils is 98% Chinese and 2% non-Chinese (Malay, Indian a nd Siamese). All the teaching staff s are Chinese except two Malay teachers. The supporting staff s are of mixed race s with Malay majority. It is located in the outskirt of a fast developing city of Kedah. The majority of its pupils live nearby and come from middle to lower income families. Most parents are working and their occupation ranged from hawkers, businessman to professionals. The school has achieved 97% and 96% passes respectively in the UPSR mathematics for the past two years (1999 & 2000).
School Motto
The school motto of School H is � diligence and respect your job � ( 勤�学�敬�业� ). This ‘ bears implications which encompass aspect s such as determination and gratitude ’ . This is also reflected in the name of the school, which means � 恒�心� ( Perseverance ) � and � 毅�力� (Persistence) � . The motto for School B is � 誠\勤�潔�毅� (Cheng Qin Jie Yi) � , whi ch means � honesty, diligence, clean and persistence � . It is thus observed that diligence and persistence seem to be the two main values emphasised by these Chinese schools. Manifesting these values into practice, perhaps there is then no surprise that hard work and a lot of practice in mathematics learning is the norm or the characteristic of the Chinese schools.
Belief of learning mathematics: practice makes perfect � 熟�能�生� 巧� �
The most pr ominent belief of learning mathematics seem to be practice make perfect or � 熟�能�生�巧� � . This belief was not only held by the school administrators, mathematics teachers but also parents and pupils of both schools. When the headmaster of school B was asked, in o rder to teach well in mathematics, what should be the focus, he gave the opinion of � doing a lot of practice� . In addition, he explained,
因�为�熟�能�生�巧�啦� ! 熟�能�生�巧� , 所�以�多�练�习�会�有�帮�助� . [Because practice makes perfect. More practice will help ] (Headmaster, School B)
The he admistress of School H also echoed the same belief:
“� 数�学�它�一�旦�会�了�它�的�概�念�之�后�,�那�么�他�多�做�了�练�习�,�自�然�就�可�以�了�啦�!� ”�
(Headmistress, school H)
According to
her, once a student understands the mathematical concepts and then practice
a lot, he/she will ‘ naturally ’ be good at mathematics.
Likewise, the mathematics teachers of both schools whom I
interviewed also shared the same belief that to be good in mathematics means
to do a lot of drill and practice as one of them explained:
我�们�的�观�点�是�这�样� , 数�学�方�面�
, 我�们�说�熟�能�生�巧� . 你�只�要�做�多�了�
, 你�就�自�然�而�然�会�做� .
好�像�应�用�题� , 每�年�的�出�题�方�式�
, 大�同�小�异� . 比�如�说� 计�算�面�积�
, 距�离� , 时�间�那�些� , 全�部�都�是�一�样�
, 方�式�大�概�大�同�小�异� ,
只�要�你�做�多�几�题� , 熟�悉�了�
, 知�道�用�什�么�技�巧� , 你�就�能�够�做�了�
. 有�时�它�的�问�题�可�能�会�变�动�一�下�
, 人�的�名�字�不�同� , 差�不�了�多�少�
, 我�们�认�为�是�这�样� . 你�要�做�对�
, 你�就�要�多�做� . 最�重�要�是�熟�能�生�巧�
.
[Our opinion is like this, in mathematics, we say practice
make perfect, when you do a lot, you will naturally know how to d o. For example,
t he word problems, every year the questions asked are almost the same, such
as calculating the area, distance, time etc are asked in nearly the same way.
As long as you do more questions, you will be familiar with the format, know
which skill to use, you w i ll sure know how to solve them. Sometimes the questions
may change a little, such as changing the name of people etc... You want to
do right, you must do a lot, and the most important is practice make perfect…�
]
(Mathematics Teacher H2)
In brief, the schoo l administrators and mathematics teachers of both schools viewed mathematics learning as � a way of mental exercise� or a skill. A lot of drill and practice do not mean rote learning. Students should be given various types of problems to solve so as to pro v ide them with various learning experience about a concept. They fully agreed and understood the importance of � concept understanding� but as mathematics teacher H2 elaborated further that,
如�果� CONCEPT UNDERSTANDING 你�没�有� PRACTICE
,�也�是�不�能�。�你� UNDERSTAND ,�你�没�有�
PRACTICE ,�你� 很�快�就�忘�记�了�,�就�是�你�要�
UNDERSTANDING 又� PRACTICE ,�两�个�一�起�,�那�么�你�
PRACTICE 久�了� , 当�然�你�会� UNDERSTAND
一�样�的�,�有�关�联�的�。�但�是�你�一�直�
PRACTICE ,�熟�能�生�巧�。�
[If only concept understanding, but you do not practice, it
’ s also not possible. You unders tand but you don ’ t practice,
you will forget very fast. You have t o understand and practice, doing both
together. As you practice more and long enough, you will surely understand,
both are related. But if you continue to practice, then practice make perfect.]
(Mathematics Teacher H2)
Thus, to these
teachers, a lot of dri lls and practice is much more important than concept
understanding as practice aid in understanding of concepts. Moreover, merely
understanding of mathematical concepts is not enough, as it needs practice to
reinforce and to enhance learning. Therefore, c o ncept understanding and practice
are both closely related and reinforce each other.
Consequently, both school authorities have encouraged the
pupils to buy additional workbooks and exercise books besides the school mathematics
textbook and activity books. Depending on the grade of the pupils, the number
of workbooks varies. For Primary one to Primary five, the pupils are required
to buy at least two additional workbooks in a year. However, for Primary Six
pupils who will be sitting for their examinations a t end of the year, they
are also encouraged to buy past year examination series, and other examination
related reference books. As highlighted by the headmistress that, practising
the past year questions will familiarise the pupils with the examination fo
r mat. This is of great importance and great help when they sit for the examination
later.
This belief on the importance of practice in mathematics
learning is also well perceived by both par ents and pupils of both schools.
When some Standard 5 pupils of Sc hool H were asked how to be good at mathematics,
their answers were:
应�该�是�多�做�练�习� . [must do a lot of exercises]
(Student H1, boy)
要�做�很�多�练�习�题� , 又�要�专�心�听�老�师�讲�课� [have to do a lot of exercises and keep full at tention to the teacher ’ s teaching]
(Student H5, girl)
Yes, it ’ s tr ue. Practice make perfect. The more they [children] practice the more they are exposed to mathematics, then they will learn better compare to those who have less experience, less practice. So it ’ s good [to] make them learn more. If they don ’ t know never m ind, [it is] up to the parents to explain. They will have better understanding and approach towards mathematics.
(Parent H4, priest)
With such a pervasive shared belief of � practice make perfect� , perhaps, there is no surprise that all the four parties als o agreed upon the importance of homework as discussed below.
Homework
In line with the belief of the importance of practice in mathematics, all the four parties agreed that it is very important to give homework for mathematics learning. Homework refers to mathematical exercises or assignments given to pupils to be completed at home or out of school lesson. According to them, doing homework will help to
给�他�们�多�练�习� [ give them more practice ]
(Parent H9, salesman)
因�为�有�帮�助�到�他�们�,�每�天�老�师�教�的�东�西�,�都�有�给�他�们�功�课�做�,�他�们�可�以�多�练�习�,�可�以�进�大�脑�。�
[because can help them, everyday whatever the teacher taught,
give them home work to do, they can then practice more and can be “�absorbed”�
by the brain]
(Par ent H3, businesswoman)
Thus, there were no parents whom we interviewed complain that the school had given too much homework to their children. Instead, three of the parents from School H felt that the amount of homework given by the school, especially for the lower primary pupils was not sufficient.
问�:�你�觉�得�老�师�给�的�功�课�
, 够�不�够�?�
[Do you think the amount of homework given by the teacher
is sufficient?]
答�:�应�该�还�不�够�,�太�少�了�。�
[should be not sufficient, too little]
问�:�为�什�么�?� [Why?]
答�:�好�像�少�了�,�他�们�学�习�方�面�会�比�较�慢�一�点�,�不�知�道�在�学�校�他�们�给�的�功�课�多�不�多�,�带�回�家�的�
HOMEWORK 会�比�较�少�一�点�。�
[like too little, their learning will slow down, (I) don ’
t know whether in school how much exercise was given to them, whatever they
brought home wa s comparatively little ]
问�:�大�概�多�少�?�
[about how many?]
答�:�有�时�两�本�罢�了�,�如�果�
COMPARE 别�的�学�校�,�别�的�学�校�功�课�比�较�多�,�好�象�做�不�完�这�样�。�
[sometimes only two books, if compared to other schools, th ey have a lot of
homework, like cannot finish.]
( Parent H2 , p hotographer)
Consequently,
these parents send their children for out-of-school tuition where the pupils
are given even more exercises to practice.
Although practice make perfect, but too much homework or
too many questions given may not really benefit the pupils, instead, according
to one of the mathematics teacher, he found that,
有�时�候�给�他�们�比�较�多�一�些�题�目�罢�了�
, 明�天�教�回�来�的�功�课�就�乱�七�八�糟�了�
, 每�一�次�都�是�这�样� . 所�有�我�们�都�给�他�们�适�量�的�
, 大�概�这�样�子�他�们�可�以�做�的�很�好�
, 那�么�我�们�就�给�这�种�题�目�
. 如�果�超�出�这�个�题�目�的�话�
, 如�果�一�天�给�他�五�十�题�的�话�
, 可�能�他�会�做�到� , 都�变�成�不�会�了�
, 全�部�错�了� . 每�次�都�遇�到�这�种�现�象�
.
[Sometimes we gave them a little more questions, what they
handed up tomorrow will be in a mess, it is always like that. So we have to
give them just sufficient amount, an amount that we estimate they can complete
nicely. If we give them more than that amount, e.g. 50 questions a day, those
who can do a lso become cannot do, all become wrong. This phenomenon is common].
(Mathematics teacher H1)
If pupils were given too many questions, they might not do it properly or they might lose their interest in mathematics. Therefore suitable amount of exercise is important. So what is the most suitable amount of exercise? One of the mathema tics teacher offer his suggestion,
我�是�通�常�,�这�个�数�学�题�目�,�我�大�概�他�们�回�家�半�个�小�时�内�可�以�做�完�,�因�为�我�们�也�考�虑�到�别�的�功�课�。� [normally I estimate if they can finish in half an hour if they bring home to do, we have to conside r that they have other subject homework to do too]
(Mathematics teacher H1)
In terms of
the amount of exercises given, the deputy head teacher of School B explained
that, the amount of exercises given varies between the good class and the poorer
one. For t he good class, questions of higher level and higher number are given.
For each unit (for example: addition), pupils are asked to do at least 5 to
6 pages of exercises. As each page consists of about 20 questions, this means
about 100 to 120 questions for e ach unit. After each unit was taught, pupils
will be given an assessment test, which consists of at least 40 questions. If
the mathematics teacher found that pupils are still weak at certain concepts,
then additional questions that related to the particul a r concepts will be
given too. Furthermore, more challenging questions which usually in the form
of problem solving will also be given to the good class pupils after they have
finished the basic drilling exercises. For the poorer class, almost the same
amo u nt of exercises will be given, but they are of lower level of difficulty.
Eve n though pupils were given such a considerable amount
of exercises to practice, no pupils whom I interviewed complained about it.
The following conversation illustrate this:
问�:�每�天� 老�师�给�很�多�练�习�吗�
? [Do your teacher give you a lot of exercises everyday?]
答�:�很�多� . [a lot ]
问�:�多�少�页� , 还�是�怎�样�
? [How many pages or how much?]
答�:�给�很�多�页� , 有�时�复�印�那�些�作�业�给�我�们�做�
. [ quite a lot, sometimes photostated copies of exercises]
问�:�你�觉�得�功�课�会�太�多�吗�
? [ Do you find the homework give too much ?]
答�:�不�会� . 不�会�啊�
, 可�以�啊� ! 可�以�很�快�做�完�啦�
! [ No. no! can finish it very fast!]
(Student B6, gi rl)
Out-of-school Tuition
The majority of the pupils in both schools took � out-of-school tuition� in mathematics. Some of them started as early as Primary one. For example, the data indicate that out of the nine parents of School H interviewed, eight of them have children taking � out-of-school tuition� in mathematics since Primary one or two . Similarly, out of the seven pupils interviewed, three of them have been taking tuition s ince Primary one . Only t wo of them did not attend tuition class because one of them was tutored by his elder brother while another by her parents (who were both teacher s) at home. It seems that both parents and pupils have strong faith in the benefit of ta king � out-of-school tuition � . As they explained,
问� : 你�觉�得�补�习�对�你�有�帮�助�吗�
? [Do you think tuition is helpful to you?]
答� : 有� . 因�为�可�以�加�强�
, 增�加�我�的�知�识� , 然�后�有�不�明�白�的�地�方�可�以�问�补�习�老�师�
[ Yes , because can improve my knowledge, anything I don ’
t understand, I can ask the tuition teacher.]
(Pupil H2, bo y, Primary 5)
我�本�身�很�忙�的�,�所�以�只�有�靠�补�习�老�师�的�时�间�来�安�排�给�他�们�多�读�而�已�。�
[I myself is very busy, so I have to depend on the tuition
teacher to get them to read more]
(Parent H6, businesswoman)
他�们�比�较�懒�散�。�我�们�要�要�求�他�们�,�他�们�就�会�做�。� [ They are relatively lazy, we need to force them, and they will do]
(Parent H7, goldsmith)
Thus, the data
reflect that pupils are happy t o have extra coaching from their tuition teachers
while some parents regarded the tuition teachers as a replacement of their parental
role in their children ’ s education.
Even th e headmistress of school H generally encourages her
pupils to take tuition outside school if their families are financially affordable.
While the deputy headmistress of School B believes that out of school tuition
is only necessary for those average or wea k pupils. She believed that t uition
could also be helpful for pupils who do not have a n y body at home to guide
them. For the clever one s , they should not be burdened with tuition. However,
she noticed that many parents today send their children for out-of-s chool tuition
because they are afraid that their children will lose out if they do not. S
ome parents send their children for tuition as early as kindergarten. She observed
that some pupils tend not to pay much attention in class because they have learnt
fa ster in their tuition class. A s a result, these pupils sometimes create
disturbance in class. This represents the possible adverse effect of out-of-school
tuition.
While the mathematics teachers of both schools generally
denied the necessity of taking out- of-school tuition, as t hey believe that
their schools have provided sufficient drill and practice for their pupils.
Nevertheless, they do believe that tuition can help those pupils who are weak
in mathematics. Anyhow, most parents and pupils of both school s seem to have
strong faith in the benefit of tuition as a way to provide more practice in
mathematics . Again, their actions match what they believe about the importance
of drill and practice in the learning of mathematics.
Memorisation of multiplication tables
Again, all the four parties: school administrators, mathematics teachers, parents and pupils of both schools agreed upon the importance of memorising multiplication tables. This is especially emphasised by the mathematics teachers and school admini strators. The deputy headmistress of School B strongly believed that if a pupi l cannot memorize multiplication tables, then it would be very difficult for him/her to do mathematics.
因�为�二�年�级�开�始� , 我�们�的�乘�法�表�就�放�进�来�了� , 如�果�乘�法�表�不�能�背�啦� , 你�不�背�的�话�啊� , 你�根�本�就�不�用�做�数�学�了� . [because from Primary Two , we have include d the reading of multiplication tables. If you can ’ t memorize the multiplication tables, then you don ’ t have to do mathematics anymore]
(deputy headmistress, School B)
In both schools, all pupils are drilled to memorize multiple tables sin ce Primary two. They s tart from multiplication of two. All pupils are expected to master the multiplication tables to 9x9 at the end of Primary Two. For those pupils of higher ability, they are encouraged to memorize un til 12x12. Some of the strategies sug gested by the mathematics teachers include:
1. reciting in class
2. peer tutoring – the better student coaches the
poorer student to recite every day before the class starts.
3. Pupils are asked to � dictate in silent � and write
down the whole multiplication table s .
Thus, generally the majority of the pupils would have mastered the multiplication tables by Primary 4 and this has somehow enhanced their learning of mathematics. For those who are still weak in memorising multiplication tables, one of the mathematics t eachers interviewed has offered other strategies as discussed below.
Culture or language advantage on mathematics
To aid memorising of multiplication tables, one senior mathematics teacher of School B (B1) has used his own creativity to design some strateg ies to help his pupils. He pointed out that in the Chinese culture, there are some cultural advantages, especially in terms of language. Besides the Chinese number system being more systematic and easier for pupils to remember, he also makes use of ‘‘ rhym e � ( 口�诀� ) and certain ‘‘ sound� of Chinese language and dialects to help pupils memorize multiplication tables and certain mathematical facts and rules. For examples:
� 有�括�号�
( ) 不�放�过�,�无�挂�号� ( ) 找�乘�除�
, ,�先�乘�除�后�加�减�
。� [got bracket don ’ t miss it, no bracket
check for x & ¸ , multiply
a nd divide before add and minus]
� 8 x
8 = 64, use the sound as related to 爸�爸�全�都�六�十�四�岁�
’ . � 我�们�就�说�你�的�爸�爸�全�都�六�十�四�岁�了�
, 然�后�那�个�爸�爸�是�不�会�错�了�
! 他�爸�爸�几�岁� , 他�直�接�就�可�以�讲�六�十�四�岁�
� . [We tell that all your fathers are 64 years old.
So when they were asked how old is your father, they will say 64] Note: � 8
� sounds as 爸�
, so 88 sound as 爸�
爸� (father).
� 7 x
7 = 49 应�该�七�七�四�十�九�才�结�婚�
[seven seven forty nine years old only get married]
� 3 x 8 = 24 比�如�说�这�个�三�八� , 怎�样�会�变�餓I死� ? Note: ‘ 三�八� ’ (san pa) in Hokkein dialect means � stupid � or � idiot � while 餓I死� means die of hunger. Therefore, * if y ou are stupid or idiot, you may die of hunger. Hokkien is a common dialect for the Chinese in the northern region of Malaysian
� 3 x
7 = 21 不�管�你�三�七�二�十�一�
[Don ’ t care three seven twenty one, we better
run!!]
� 所�有�五�的�
, 你�就�是�五�零� , 五�零� , 五�零�
, 其�他�号�码�不�可�以�写�
[ for multiplication of five, i t is always 5 & 0, others
don ’ t write]
Thus, by taking advantage of language coupled with his creativities, mathematics teacher B1 has helped his pupils to memorize multiplication tables in a much more fun and easy way.
Implications and Conclusion
The f indings
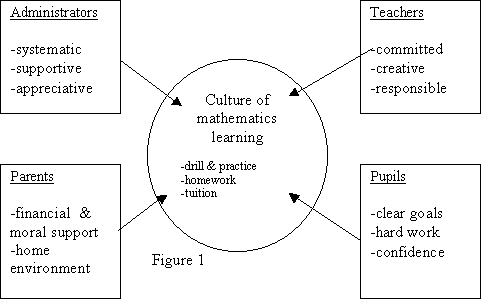
so far thus illuminate that all the four parties of these schools: administrators,
mathematics teachers, parents and pupils, seem to share a similar belief of
� practice make perfect� . Consequently all of them work towards this goal by
providing an d supporting a learning environment that stresses on � practice�
, � tuition� and � memorisation of multiplication tables� . The administrators
encourage the pupils to buy extra workbooks and exercise books as well as to
go for out-of-school tuition. The mathem a tics teachers provide a lot of drills
and practice in school. The parents provide financial and moral support to achieve
the same vision. The pupils too have no complaint over the heavy workload. They
seem to share the same confidence that as long as they work hard, practice a
lot, they are going to achieve good results in mathematics. Findings of this
study thus, in part, reconfirm findings by Munirah and Lim (1996) that most
Chinese medium schools favour more drill and practice, as well as more homework
a nd tuition.
However, this study also indicates that a lot of drill and
practice do not mean rote learning or learning without understanding. Students
are first taught a mathematical concept, and then followed by doing many similar
exercises with increasin g degrees of difficulties. Exercises that provide similar
practice or related to a common concept or skill will strengthen students ’
understanding of the concept or mastery of the skill. In fact, these drill and
practice may be considered as aiding the st u dents to build up � a schema�
(Skemp, 1971). After constructing a schema, giving exercises with increasing
difficulties will help students to expand their schema or making generalisation.
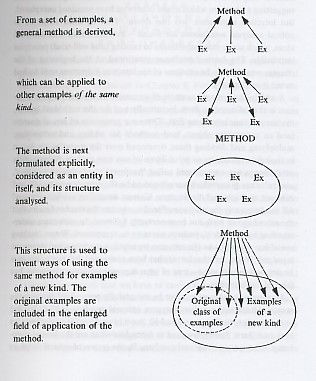
This is as suggested by Skemp as a powerful of mathematical generalis a tion
as illustrated below:

Moreover, the concerted efforts of all parties seem to shape
the culture of mathematics learning in these schools, and consequently warrant
a higher achievement in mathematics. In brief, the culture of mathematics learning
as related to all the four parties may be depicted as in Figure 1.
In addition, there exist several advantages in terms of culture
or language, which may not be able to apply to all pupils as not all pupils
study mathematics using the same m edium of instruction. However, the findings
show that it is up to the creativity of the teachers to find similar advantages
in other language to help pupils, such as to memorize the multiplication tables,
and thus enhanced their mathematical skills as wel l as their confidence and
interest in mathematics.
References
Bennet, C. I. (1990). Comprehensive multicultural
education . Allyn and Bacon.
Bishop, A.J. (1988). Mathematical
Enculturation-a cultural perspective on mathematics education
. Netherlands: Kluwer Academic Publishers.
Ernest, P. (1991). The philosophy of mathematics education . London: The Falmer Press.
Lim, Soo Kheng & Chan, Toe Boi (1993). A case study comparing the
learning of mathematics among Malay pupils in primary national school and primary
national type [Chinese} schools. Journal of Science
and Mathematics Education in South East Asia, 16
(2), 49-53.
Munirah.Ghazali & Lim, Chap Sam. (1996). Chapter 7: Primary
mathematics. In Lee, Molly., Yoong, Suan, Loo, Seng Piew., Khalid, Khadijah.,
Ghaza li, Munirah., & Lim, Chap Sam. (1996).
Students' orientation towards science and mathematics: Why are enrolments
falling? (Monograph series number 1/96). Penang,
Malaysia: Universiti Sains Malaysia.
Skemp, R. (1971). The psychology
of learning mathematics . Penguin Books.
Yoong Suan, Santhiran Raman, Fatimah Salleh, Lim Chap Sam,
Munirah Ghazali (1997). Basic number concepts acquisition
in mathematics learning: an exploratory cross-cultural study
. Programme Innovation, Excellence and Research (PIER) grant. (research report)