WHAT IS THE PHILOSOPHY OF MATHEMATICS EDUCATION?

Paul Ernest

University of Exeter, United Kingdom

<P.Ernest@ex.ac.uk>

This question (what is the philosophy of mathematics education?) provokes a number of reactions, even before one tries to answer it. Is it a philosophy of mathematics education, or is it the philosophy of mathematics education? Use of the preposition ‘a’ suggests that what is being offered is one of several such perspectives, practices or areas of study. Use of the definite article ‘the’ suggests to some the arrogation of definitiveness to the account given.[1] In other words, it is the dominant or otherwise unique account of philosophy of mathematics education. However, an alternative reading is that ‘the’ refers to a definite area of enquiry, a specific domain, within which one account is offered. So the philosophy of mathematics education need not be a dominant interpretation so much as an area of study, an area of investigation, and hence something with this title can be an exploratory assay into this area. This is what I intend here.

Moving beyond the first word, there is the more substantive question of the reference of the term ‘philosophy of mathematics education’. There is a narrow sense that can be applied in interpreting the words ‘philosophy’ and ‘mathematics education’. The philosophy of some area or activity can be understood as its aims or rationale. Mathematics education understood in its simplest and most concrete sense concerns the activity or practice of teaching mathematics. So the narrowest sense of ‘philosophy of mathematics education’ concerns the aims or rationale behind the practice of teaching mathematics. ‘What is the purpose of teaching and learning mathematics?’ is an important question. I have added learning to it because learning is inseparable from teaching. Although they can be conceived of separately, in practice a teacher presupposes one or more learners. Only in pathological situations can one have teaching without learning, although of course the converse does not hold. Informal learning is often self directed and takes place without explicit teaching.

Returning to the question of the aims of teaching mathematics it is important to note that aims, goals, purposes, rationales, etc, do not exist in a vacuum. They belong to people, whether individuals or social groups. Indeed since the teaching of mathematics is a widespread and highly organised social activity, and even allowing for the possibility of divergent multiple aims and goals among different persons, ultimately these aims, goals, purposes, rationales, and so on, need to be related to social groups and society in general. Aims are expressions of values, and thus the educational and social values of society or some part of it are implicated in this enquiry. In addition, the aims discussed so far are for the teaching of mathematics, so the aims and values centrally concern mathematics and its role and purposes in education and society.

So already by considering the narrow meaning of philosophy of mathematics education, the issues of the teaching and learning of mathematics, the underlying aims and rationales of this activity, the roles of the teacher, learner, and mathematics in society and the underlying values of the relevant social groups are implicated. This resembles the issues arising from applying Schwab's (1961) four 'commonplaces of teaching' to the mathematics curriculum. These are the subject (mathematics), the learner of mathematics, the mathematics teacher, and the milieu of teaching, including the relationship of mathematics teaching and learning, and its aims, to society in general. I shall return to these issues and areas of enquiry.

However there is a missing element from philosophy of mathematics education that a broader interpretation brings into play, namely that of philosophy. The metonymic structure of the term ‘philosophy of mathematics education’ brings ‘philosophy’ and ‘mathematics’ together, foregrounding the philosophy of mathematics. The philosophy of mathematics is undoubtedly an important aspect of philosophy of mathematics education, especially in the way that the philosophy of mathematics impacts on mathematics education. This is part of the missing element.

In his essay on the subject of the philosophy of mathematics education Stephen Brown (1995) asks a very pertinent question by posing a trichotomy. Is the philosophical focus or dimension:

1.      Philosophy applied to or of mathematics education?

2.      Philosophy of mathematics applied to mathematics education or to education in general?

3.      Philosophy of education applied to mathematics education?

Figure 1 illustrates these alternatives diagrammatically in a simplified way.

Figure 1: Different applications of philosophy to mathematics education

 

 

 

 

 

 

 

 

 

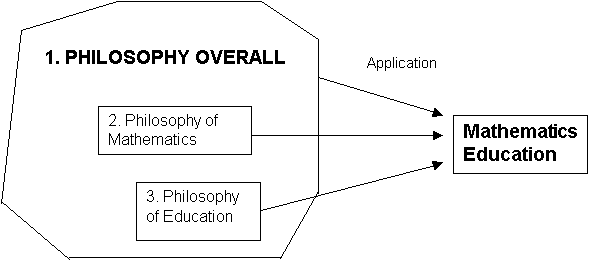Each of these three possible ‘applications’ of philosophy to mathematics education represents a different focus, and might very well foreground different issues and problems. However, Figure 1, of course, raises more questions than it answers. It illustrates that applications can be made either of philosophy or of two special branches of it. However what is such an application? The diagram might be taken to suggest that there are substantive bodies of knowledge and applicational activities connecting them, whereas philosophy, mathematics education and other domains of knowledge encompass processes of enquiry and practice, personal knowledge, and as well as published knowledge representations. They are not simply substantial entities in themselves, but complex relationships and interactions between persons, society, social structures, knowledge representations and communicative (and other) practices.

In particular, philosophy is about systematic analysis and the critical examination of fundamental problems. It involves the exercise of the mind and intellect: thought, enquiry, reasoning and its the results, judgement, conclusions and belief or beliefs. There are so many ways in which such processes as well as the substantive theories, concepts and results of past enquiry can be applied to and within mathematics education.

At the very least, this suggests that the philosophy of mathematics education should not only attend to the philosophy of mathematics. Stephen Brown (1995) suggests that it should also look to the philosophy of Schwab's other commonplaces of teaching: the learner, the teacher, and the milieu or society.  So we also have the philosophy of learning (mathematics), the philosophy of teaching (mathematics) and the philosophy of the milieu or society (with respect to mathematics and mathematics education) as further elements to consider.

Looking at each of these four commonplaces in turn, a number of questions can be posed, as issues for the philosophy of mathematics education to address, including the following.

1. WHAT IS MATHEMATICS?

What is mathematics, and how can its unique characteristics be accommodated in a philosophy? Can mathematics be accounted for both as a body of knowledge and a social domain of enquiry? Does this lead to tensions? What philosophies of mathematics have been developed? What features of mathematics do they pick out as significant? What is their impact on the teaching and learning of mathematics? What is the rationale for picking out certain elements of mathematics for schooling? How can (and should) mathematics be conceptualised and transformed for educational purposes? What values and goals are involved? Is mathematics value-laden or value-free? How do mathematicians work and create new mathematical knowledge? What are the methods, aesthetics and values of mathematicians? How does history of mathematics relate to the philosophy of mathematics? Is mathematics changing as new methods and information and communication technologies emerge? 

This already has begun to pose questions relating to the next area of enquiry.

2. HOW DOES MATHEMATICS RELATE TO SOCIETY?

How also does mathematics education relate to society? What are the aims of mathematics education (i.e., the aims of mathematics teaching)? Are these aims valid? Whose aims are they? For whom? Based on which values? Who gains and who loses? How do the social, cultural and historical contexts relate to mathematics, the aims of teaching, and the teaching and learning of mathematics? What values underpin different sets of aims? How does mathematics contribute to the overall goals of society and education? What is the role of the teaching and learning of mathematics in promoting or hindering social justice conceived in terms of gender, race, class, ability and critical citizenship? Is anti-racist mathematics education possible and what does it mean? How is mathematics viewed and perceived in society? What impact does this have on education? What is the relationship between mathematics and society? What functions does it perform? Which of these functions are intended and visible? Which functions are unintended or invisible? To what extent do mathematical metaphors (e.g., profit and loss balance sheet) permeate social thinking? What is their philosophical significance? To whom is mathematics accountable?

3. WHAT IS LEARNING (MATHEMATICS)?

What assumptions, possibly implicit, underpin views of learning mathematics? Are these assumptions valid? Which epistemologies and learning theories are assumed? How can the social context of learning be accommodated? What are constructivist, social constructivist and other theories of learning mathematics? Do they have any impact on classroom practice? What elements of learning mathematics are valuable? How can they be and should they be assessed? What feedback loops do different forms of assessment create, impacting on the processes of teaching and learning of mathematics? What is the role of the learner? What powers of the learner are or could be developed by learning mathematics? How does the identity of the learner change and develop through learning mathematics? Does learning mathematics impact on the whole person for good or for ill? How is the future mathematician and the future citizen formed through learning mathematics? How important are affective dimensions including attitudes, beliefs and values in learning mathematics? What is mathematical ability and how can it be fostered? Is mathematics accessible to all?

4. WHAT IS TEACHING (MATHEMATICS)?

What theories and epistemologies underlie the teaching of mathematics? What assumptions, possibly implicit, do mathematics teaching approaches rest on? Are these assumptions valid? What means are adopted to achieve the aims of mathematics education? Are the ends and means consistent? What methods, resources and techniques are, have been, and might be, used in the teaching of mathematics? What theories underpin the use of different information and communication technologies in teaching mathematics? What sets of values do these technologies bring with them, both intended and unintended? What is it to know mathematics in satisfaction of the aims of teaching mathematics? How can the teaching and learning of mathematics be evaluated and assessed? What is the role of the teacher? What range of roles is possible in the intermediary relation of the teacher between mathematics and the learner?  What are the ethical, social and epistemological boundaries to the actions of the teacher? What mathematical knowledge does the teacher need? What impact do the teacher’s beliefs, attitudes and personal philosophies of mathematics have on practice? How should mathematics teachers be educated? What is the difference between educating, training and developing mathematics teachers? What is (or should be) the role of research in mathematics teaching and the education of mathematics teachers?

One further set of questions for the philosophy of mathematics education goes beyond  Schwab's four commonplaces of teaching, which were primarily about the nature of the (mathematics) curriculum. This further set concerns the status of mathematics education as a field of knowledge and coming to know in it.

5. WHAT IS THE STATUS OF MATHEMATICS EDUCATION AS KNOWLEDGE FIELD?

What is the basis of mathematics education as a field of knowledge? Is mathematics education a discipline, a field of enquiry, an interdisciplinary area, a domain of extra-disciplinary applications, or what? What is its relationship with other disciplines such as philosophy, sociology, psychology, linguistics, etc.? How do we come to know in mathematics education? What is the basis for knowledge claims in research in mathematics education? What research methods and methodologies are employed and what is their philosophical basis and status? How does the mathematics education research community judge knowledge claims? What standards are applied? What is the role and function of the researcher in mathematics education? What is the status of theories in mathematics education? Do we appropriate theories and concepts from other disciplines or ‘grow our own’? How have modern developments in philosophy (post-structuralism, post-modernism, Hermeneutics, semiotics, etc.) impacted on mathematics education? What is the impact of research in mathematics education on other disciplines? Can the philosophy of mathematics education have any impact on the practices of teaching and learning of mathematics, on research in mathematics education, or on other disciplines?

These five sets of questions encompass, in my view, most of what is important for the philosophy of mathematics education to consider and explore. These sets are not wholly discrete, as various areas of overlap reveal. Nor are the questions systematically derived. Rather they originate from ‘brainstorming’, and other thinkers would probably add further questions or even further sets of questions, and might background some of the issues raised above.[2] Hence no claim for either completeness or even complete relevance can be made for them. Some of the questions are not essentially philosophical, in that they can also be addressed and explored in ways that foreground other disciplinary perspectives, such as sociology. However, in my view, when such questions are approached philosophically, they become part of the business of the philosophy of mathematics education. And often to exclude certain questions ab initio is to adopt and promote a particular philosophical position, i.e., a particular philosophy of mathematics education.  

Of course the question of what and where are the boundaries between philosophy, sociology, anthropology, psychology is yet another area of philosophical enquiry, and one that is much disputed. The traditional clear-cut ‘division of labour’, i.e., marking out of discipline boundaries has been challenged by poststructural, postmodern, and other philosophies and theories about knowledge. This is an issue that impacts particularly on the fifth set of questions listed above. 

Controversies in the Philosophy of Mathematics Education

The philosophy of mathematics education could be imagined to be a dry and overly academic domain. But there are issues central to it that have sparked great controversy within it in the past decade or two. Within the five clusters of questions identified above some selected controversies are as follows.

1. Philosophy of Mathematics

As one of the oldest sciences, and as the paradigm of certain and cumulative knowledge, mathematics and its philosophy seems an unlikely area for controversy. But currently the so-called ‘Science Wars’ are raging, mostly in USA, but also in other English-speaking countries, about philosophical views of science and mathematics. Although primarily ignited between realist and social constructivist or science studies accounts of the nature of science, the heated debate has also spilled over into the domain of mathematics. Foundationalists and absolutists, on the one hand, want to maintain that mathematics is certain, cumulative and untouched by social interests or developments beyond the normal patterns of historical growth. Fallibilists, humanists, relativists and social constructivists, on the other hand, have been arguing that mathematics is through and through historical and social, and that there are cultural limitations to its claims of certainty, universality and absoluteness. This controversy can become very heated and even emotionally charged, as correspondence in the American Mathematical Monthly and Mathematical Intelligencer illustrates. Barnard and Saunders (1994) illustrate the negative reaction of some British mathematicians to the claims of fallibilism in philosophy of mathematics.

2. Aims of Mathematics Education

The aims of mathematics education can be a hotly contested area, especially when new curricula are being developed or disseminated through a national or regional education system. In Ernest (1991) I identified the aims of five different groups contesting the nature and aims of the British (for England Wales) National Curriculum in mathematics, during the late 1980s and early 1990s. In summary, these five groups and their aims were as follows:

1.      Industrial Trainer aims -  'back-to-basics': numeracy and social training in obedience (authoritarian),

2.      Technological Pragmatist aims -  useful mathematics to the appropriate level and knowledge and skill certification (industry-centred),

3.      Old Humanist aims -  transmission of the body of mathematical knowledge (mathematics-centred),

4.      Progressive Educator aims -  creativity, self- realisation through mathematics (child-centred),

5.      Public Educator aims - critical awareness and democratic citizenship via mathematics (social justice centred).

These aims are best understood as part of an overall ideological framework that includes views of knowledge, values, society, human nature as well as education. In Britain, the contestation between these groups was largely behind the scenes, although sometimes it spilled over into the public arena when interest groups sought to gain public support for their positions. My analysis suggested that the first three interest groups formed a powerful and largely victorious alliance in 1980s and 1990s Britain. This forced the aims of group 4 (Progressive Educators) to be compromised and filtered through those of group 2 (Technological Pragmatist) in order to have an impact on the curriculum. The aims of group 5 (Public Educators) were eliminated in this struggle, and had no impact at all. Similar struggles and contestations have been noted in other countries too.

3. Theories of Learning Mathematics

Elements of constructivist theories of learning can be traced back to antiquity, although perhaps the most influential modern source is Jean Piaget. None of this is very controversial. However, in the Summer of 1987 constructivism burst onto the international scene at the exciting and controversial Eleventh International Conference on the Psychology of Mathematics Education in Montreal. A number of distinguished speakers attempted a critique of radical constructivism, most notably the strong version due to Ernst von Glasersfeld (1995). As he had noted “To introduce epistemological considerations into a discussion of education has always been dynamite” (Glasersfeld 1983: 41). Ironically, the attacks on radical constructivism at that conference, which were intended to expose the weaknesses of the position fatally, served instead as a platform from which it was launched to widespread international acceptance and approbation. This is not without continuing strong critiques of constructivism from mathematicians and others (e.g., Barnard and Saunders 1994).   

Since then, yet further controversy has erupted between different versions of constructivism, most notably radical constructivism versus social constructivism (Ernest 1994a), as well as powerful critiques of constructivism learning theory both within science and mathematics education, and from without.

4. Mathematics Teaching

The teaching of mathematics is also an area in which there can be heated and controversial clashes of philosophy or ideologies. Among the ‘hot’ areas and issues are the following

1.      Mathematical pedagogy - problem solving and investigational approaches to mathematics versus traditional, routine or expository approaches? Such oppositions go back, at least, to the controversies surrounding discovery methods in the 1960s.

2.      Technology in mathematics teaching – should electronic calculators be permitted or do they interfere with the learning of number and the rules of computation? Should computers be used as electronic skills tutors or as the basis of open learning? Can computers replace teachers, as Seymour Papert has suggested?

3.      Mathematics and symbolisation – should mathematics be taught as a formal symbolic system or should emphasis be put on oral, mental and intuitive mathematics including child methods?

4.      Mathematics and culture – should traditional mathematics with its formal tasks and problems be the basis of the curriculum, or should it be presented in realistic, authentic, or ethnomathematical contexts?

Each of these issues and oppositions has been the basis of heated debate and contestation world wide, and rests on philosophical issues and assumptions.

5. Research Methodologies  in Mathematics Education

Traditionally research in mathematics education utilised the methodologies of psychological, agro-biological and generally the styles of the scientific research paradigm. This typically makes use of certain philosophical assumptions about what there is (ontology), how and what we can know (epistemology) and the appropriate methods for gaining and testing knowledge (methodology). The scientific research paradigm normally frames hypotheses to test against empirical data gathered as objectively as possibly, often quantitative data. Thus its approach is to try to discover and test empirical laws and generalisations.

In contrast, the interpretative research paradigm has a contrasting set of philosophical assumptions (ontological, epistemological, methodological) and is modelled after the ‘softer’ human sciences. It seeks to explore real human and social situations and uncover the meanings, understandings and interpretations of the actors involved. Typically it is more exploratory than confirmatory.

Historically, in mathematics education research, and in the wider educational research community, there has been conflict between supporters of these two main research outlooks and paradigms, as the newer interpretative research sought to establish itself in a field dominated by scientific research.[3] This conflict was termed the ‘Paradigm Wars’ by Gage (1989). Such conflicts have been manifested by ‘gatekeepers’ choosing what papers to accept for conferences and journals, and what projects to fund; and thus have involved the exercise of power, of considerable significance for researchers in mathematics education. Although most researchers are by now aware of the validity of both approaches and styles, when conducted properly, nevertheless conflicts in personal judgements about such validity still arise periodically.

This brief and selective account of controversies in mathematics education research does not really indicate the strength of feelings involved. Conflicts sparked by philosophical controversies around philosophies of mathematics, the aims, learning theories, teaching approaches, and research paradigms in mathematics education continue to arise. Often this occurs when opponents fail to realise it is their underlying philosophies, assumptions and ideologies that are in conflict, not their overt proposals or claims. An awareness of the multi-dimensional philosophical issues and assumptions underpinning research in mathematics education, something that the philosophy of mathematics education can bring, can help to forestall, minimise and sometimes resolve such conflicts and misunderstandings.

Linking Philosophies of Mathematics and Mathematical Practice[4]

One of the central issues for the philosophy of mathematics education is the link between philosophies of mathematics and mathematical practices. A widespread claim is that there is a strong if complex link between philosophy and pedagogy. As Steiner (1987: 8) says “all more or less elaborated conceptions, epistemologies, methodologies, philosophies of mathematics (in the large or in part) contain - often in an implicit way - ideas, orientations or germs for theories on the teaching and learning of mathematics.”

In the philosophy of mathematics there is a range of perspectives which may be termed ‘absolutist’. These view mathematics as an objective, absolute, certain and incorrigible body of knowledge, which rests on the firm foundations of deductive logic. Among twentieth century perspectives in the philosophy of mathematics, Logicism, Formalism, and to some extent Intuitionism, may be said to be absolutist in this way (Ernest 1991, 1998). Absolutist philosophies of mathematics are not descriptive philosophies, but are concerned with the epistemological project of providing rigorous systems to warrant mathematical knowledge absolutely (following the crisis in the foundations of mathematics of around 1900). Many of the claims of these philosophies – let me refer to them together as absolutism - follow from the identification of mathematics with rigid logical structure introduced for epistemological purposes. Thus according to absolutism mathematical knowledge is timeless, although we may discover new theories and truths to add; it is superhuman and ahistorical, for the history of mathematics is irrelevant to the nature and justification of mathematical knowledge; it is pure isolated knowledge, which happens to be useful because of its universal validity; it is value-free and culture-free, for the same reason.

Thus although it exceeds its intended scope, absolutism suggests a philosophically sanctioned image of mathematics as rigid, fixed, logical, absolute, inhuman, cold, objective, pure, abstract, remote and ultra-rational. If this is how many philosophers, mathematicians and teachers view their subject, small wonder that it is also the image communicated to the public, and in school. In my view, the philosophy of mathematics is at least partly to blame for this negative image, because of its twentieth century obsession with epistemological foundationalism.

An absolutist-like view may be communicated in school by giving students mainly unrelated routine mathematical tasks which involve the application of learnt procedures, and by stressing that every task has a unique, fixed and objectively right answer, coupled with disapproval and criticism of any failure to achieve this answer. This may not be what the mathematician recognises as mathematics, but a result is nevertheless an absolutist-like conception of the subject (Buerk 1982). In some cases the outcome is also a strongly negative affective response to mathematics too, sometimes termed ‘mathephobia’ (Buxton 1981, Maxwell 1989).

However, in the past few decades a new wave of ‘fallibilist’ philosophies of mathematics has been gaining ground, and these propose a different and opposing image of mathematics as human, corrigible, historical and changing (Davis and Hersh 1980, Ernest 1994b, Lakatos 1976, Tymoczko 1986). Fallibilism views mathematics as the outcome of social processes. Mathematical knowledge is understood to be eternally open to revision, both in terms of its proofs and its concepts. Consequently this view embraces the practices of mathematicians, its history and applications, the place of mathematics in human culture, including issues of values and education as legitimate philosophical concerns. The fallibilist view does not reject the role of logic and structure in mathematics, just the notion that there is a unique, fixed and permanently enduring hierarchical structure. Instead it accepts the view that mathematics is made up of many overlapping structures which, over the course of history, grow, dissolve, and then grow anew, like trees in a forest (Steen 1988).

Fallibilism does reject the absolutist image of mathematics as a body of pure and perfect abstract knowledge which exists in a superhuman, objective realm (Davis 1972). Instead mathematics is associated with sets of social practices, each with its history, persons, institutions and social locations, symbolic forms, purposes and power relations. Thus academic research mathematics is one such practice (or rather a multiplicity of shifting, interconnected practices). Likewise each of ethnomathematics and school mathematics is a distinct set of such practices. They are intimately bound up together, because the symbolic productions of one practice is recontextualised and reproduced in another (Dowling 1988).  

However, it is important to distinguish between a fallibilist (or absolutist) epistemology of mathematics, and a fallibilist (or absolutist) account of the nature of mathematics. The former is a strictly defined philosophical position concerning the epistemological foundation and justification of mathematical knowledge. The latter is a looser descriptive account of mathematics in a broader sense. Usually these are linked, but strictly speaking, it is possible for an epistemological absolutist to promote aspects of a fallibilist view of the nature of mathematics: including, for example such views as: mathematicians are liable to error and publish flawed proofs, humans can discover mathematical knowledge through a variety of means, the concepts of mathematics are historical constructs (but its truths are objective), a humanised approach to the teaching and learning of mathematics is advisable, etc. Likewise, an epistemological fallibilist might argue that although mathematical knowledge is a contingent social construction, so long as it remains accepted by the mathematical community it is fixed and should be transmitted to learners in this way, and that questions of school mathematics are uniquely decidable as right or wrong with reference to its conventional corpus of knowledge. My argument is that there is a strong analogy between epistemological absolutism, absolutist views of the nature of mathematics, and the cold, objectivist popular image of mathematics. But these three perspectives remain distinct and no logically necessary connection between them exists, even if the analogy is strong.

Two philosophical views of mathematics have been described. Which of them reflects the image of mathematics in school? It must be said that the experience some learners have from their years of schooling confirms the absolutist image of mathematics as cold, absolute and inhuman. It is far from uncommon for teachers and others and the experience of learning itself to confirm this view. Such an image is often, but not always, associated with negative attitudes to mathematics. A counterexample arose in my research on student teacher’s attitudes and beliefs about mathematics. I found a subgroup of mathematics specialists who combined absolutist conceptions of the subject with very positive attitudes to mathematics and its teaching. However amongst non-mathematics-specialist future primary school teachers I found a loose correlation between fallibilist conceptions and positive attitudes to mathematics and its teaching (Ernest 1988, 1989b). Thus the connections even just between beliefs and attitudes to mathematics are complex and multifaceted.

Research on children’s attitudes towards mathematics in the past two decades shows fairly widespread liking of the school subject, certainly in the years of elementary schooling (Assessment of Performance Unit 1985). In the later years of schooling attitudes in general become more neutral, although extreme negative attitudes are relatively rare. Presumably this downturn in attitudes is due to such things as adolescence, peer-attitudes, the impact of competitive examinations, not to mention the image of mathematics conveyed in and out of school.

However, the image of mathematics communicated in many enlightened schools and colleges is not the absolutist one and certainly does not have to be that way anywhere. Influential inquiries into the teaching of mathematics have propounded humanised and anti-absolutist (if not wholeheartedly fallibilist) views of school mathematics (Cockcroft 1982, NCTM 2000). The weight of informed educational opinion has likewise supported the progressive reform of mathematics in line with such views, although there has also been a backlash from mathematicians and more conservative thinkers (Riley 1998)

An important issue for education is the relationship between mathematics and values, especially since the popular image of mathematics is clearly value-laden. The feminist researcher Gilligan (1982) has offered a theory of values, distinguishing stereotypically feminine values (termed ‘connected’), from stereotypically masculine values (termed ‘separated’). The ‘connected’ position is based on and valorises relationships, connections, empathy, caring, feelings and intuition, and tends to holistic and human-centred in its concerns. The ‘separated’ position valorises rules, abstraction, objectification, impersonality, unfeelingness, dispassionate reason and analysis, and tends to be atomistic and thing-centred in focus.

Although we are one species and male/female differences are not as profound as our commonalities, reviews of empirical evidence suggest that there are significant differences by late adolescence and adulthood (Larrabee 1993), and girls are more likely to be empathetic than boys in exhibiting emotional reactions to another’s feelings (Hoffman 1977). Likewise, separated values have come to dominate many institutions and structures, including mathematics and science, especially in Anglophone and Protestant countries. Many people have come to feel that mathematics is cold, hard, uncaring, impersonal, rule-driven, fixed and stereotypically masculine. Evidently there is a strong parallel between the absolutist conception of mathematics, the negative popular view of mathematics, and separated values. Likewise, a second parallel exists between the fallibilist conception of mathematics, connected values and the humanistic image of mathematics promoted by modern progressive mathematics education as accessible, personally relevant and creative (Cockcroft 1982, NCTM 2000).

The second parallel can be used to improve accessibility and the public image of mathematics, although it should also be recognised that the absolutist image of mathematics attracts some people to it. Many mathematicians and others love mathematics for its absolutist features. It is both consistent and common for teachers and mathematicians to hold an absolutist view of mathematics as neutral and value free, but to regard mathematics teaching as necessitating the adoption of humanistic, connected values. This raises again the issue of the relationship between philosophies of mathematics, values and teaching.

A widely accepted position is that “All mathematical pedagogy, even if scarcely coherent, rests on a philosophy of mathematics.” (Thom 1973: 204). Other articulations stress both that teaching approaches in mathematics incorporate assumptions about the nature of mathematics, and that any philosophy of mathematics has classroom consequences (Hersh 1979, Steiner 1987). Empirical research (e.g. Cooney 1988) has confirmed claims that “teachers' views, beliefs and preferences about mathematics do influence their instructional practice” (Thompson 1984: 125). Thus it may be argued that any philosophy of mathematics (including personal philosophies) has many educational and pedagogical consequences when embodied in teachers’ beliefs, curriculum developments, or examination systems. Elsewhere I have argued that teachers’ personal philosophies of mathematics, understood as part of their overall epistemological and ethical framework, impact on their espoused conceptions of teaching and learning mathematics. These in turn, subject to the constraints and opportunities of the social context of practice, give rise to the realised theories of learning mathematics, teaching mathematics, and the related use of mathematical texts and curriculum materials in the classroom (Ernest, 1989a). Such a model is partially validated by empirical work.

However classroom consequences are not in general strictly logical implications of a philosophy, and additional values, aims and other assumptions are required to reach such conclusions (Ernest 1991, 1994c). Because the link is not one of logical implication, it is theoretically possible to consistently associate a philosophy of mathematics with almost any educational practice or approach. Both a neo-behaviourist or cognitivist (such as Ausubel 1968) and a radical constructivist (such as Glasersfeld 1995) may be concerned to ascertain what a child knows before commencing teaching, despite having diametrically opposite epistemologies (absolutist and fallibilist, respectively). Likewise a traditional purist mathematician and a social constructivist may both favour a multicultural approach to mathematics, but for different reasons (the former perhaps to humanise mathematics, the latter to show it as the social construction of all of humanity for social justice reasons).

Although there is no logical necessity for, say, a transmission-style pedagogy to be associated with an absolutist, objectivist epistemology and philosophy of mathematics, such associations often are observed (Ernest 1988, 1991). This is presumably due to the resonances and sympathies between different aspects of a person's philosophy, ideology, values and belief-systems. These form links and associations and become restructured in moves towards maximum coherence and consistency, and ultimately towards integration of the personality. (Of course compartmentalisation and ‘splitting’ are also possible.)

A simplified model (Figure 2) illustrates how the value-position of a teacher, curriculum development or school plays a vital role in mediating between personal philosophies of mathematics, and the image of mathematics communicated in the classroom. Figure 2 shows how an absolutist philosophy of mathematics combined with separated values can give rise to an separated view of school mathematics.

Figure 2: The Simplified Relations between Personal Philosophies of Mathematics, Values and Classroom Image of Mathematics.

Absolutist Philosophy of Mathematics	æ            ÷	Fallibilist Philosophy of Mathematics
ê	æ÷	ê
Separated Values	÷            æ	Connected Values
ê       ò	(‘crossing over’)	â       ê
Separated view of school mathematics		Connected view of school mathematics
ê       ò		â       ê
Constraints and Opportunities afforded by Social Context
ê       ò	å  í	â       ê
Separated Mathematics Classroom practice	(‘strategic compliance’)	Humanistic Mathematics Classroom practice

This, subject to the constraints and opportunities afforded by social context of schooling, often results in separated mathematics classroom practice. Likewise, a fallibilist philosophy of mathematics combined with connected values can give rise to a connected view of school mathematics. Subject to the same constraints, this can result in a humanistic mathematics classroom practice. These two possible sets of relations are shown by bold vertical arrows. They represent the most straightforward relationships between philosophies, values and mathematics classroom practices. 

Figure 2 also illustrates ‘crossing over’: how an absolutist philosophy of mathematics if combined with connected values can give rise to a connected view of school mathematics. This, subject to social constraints, may be realised as a connected classroom image of mathematics. A deep commitment to the ideals of progressive mathematics education can and frequently does co-exist with a belief in the objectivity and neutrality of mathematics, especially amongst mathematics teachers and educators. Fallibilism has no monopoly on this. In cases like these, connected values are often associated with education and the conception of school mathematics, rather than with academic (mathematicians’) mathematics. This is illustrated in the figure by the thin black arrows.

It is theoretically possible that a fallibilist philosophy of mathematics can combine with separated values, resulting in a separated view of school mathematics. This, subject to contextual constraints and opportunities, can give rise to a separated mathematics classroom practice. This is shown by the outline arrows, and is probably infrequent, because of the common association of fallibilism with progressive pedagogical views in the mathematics education community.

Finally, it is possible for the various constraints of the social context of schooling to be so powerful that a teacher with connected values and a humanistic view of school mathematics is forced into ‘strategic compliance’ (Lacey 1977), resulting in a separated mathematics classroom practice. This is indicated in Figure 2 by the bold and thin arrows deviating left towards the separated classroom practice following the impact of the social context. This practice may originate with either an absolutist philosophy (thin arrows), or a fallibilist philosophy (bold arrows), but in both cases ‘crosses over’. Empirical research has confirmed that teachers with very distinct personal philosophies of mathematics (absolutist and fallibilist) have been constrained by the social context of schooling to teach in a traditional, separated way (Lerman 1986).

I suggest that values as well as beliefs and philosophies play a key role in determining the underlying images and philosophies embodied in mathematics classroom practice. This is not surprising, since such values are realised in the type of teacher-pupil relations, the degree of competitiveness, the extent of negative weight placed on errors, the degree of public humiliation experienced in consequence of failure, and other such factors which powerfully impact on learners’ attitudes, self-esteem and images of mathematics.

Much work in the philosophy of mathematics education pertains to exploring the link between the philosophies of mathematics implicit in teachers' beliefs, in texts and the mathematics curriculum, in systems and practices of mathematical assessment and in mathematics classroom practices and ethos, and the results with learners. While much progress has been made in illuminating such influences, it is clear that the relationships are complex and non-deterministic.

In this essay I have explored a number of dimensions of the philosophy of mathematics education, what it is, and what some of its implications for the classroom might be. The central concern is that of inquiring into and questioning some of the presuppositions underlying theories and research in mathematics education and the practices of teaching and learning mathematics. There is a growing literature on the philosophy of mathematics education, e.g., Skovsmose (1994), in addition to the works already cited. Studies such as Kilpartrick and Sierpinska (1998) reflect philosophically on mathematics education overall as a research domain. There is also The Philosophy of Mathematics Education Journal available via the web (at <http://www.ex.ac.uk/~PErnest/>)  

One concern that is illuminated by this enquiry is the relatively weak link between the philosophy of education and mathematics education. This is a relationship that needs to be more actively explored and developed. Like mathematics, mathematics education has too much of a tendency to isolate it from adjacent areas of knowledge and enquiry. How often, for example, do we look to developments in science education? The philosophy of mathematics education is one approach that should facilitate the building of links with other areas of knowledge and research. This essay suggests a number of directions in which we could turn our gaze to begin to do this.   

References

Assessment of Performance Unit (1985) A Review of Monitoring in Mathematics 1978 to 1982 (2 volumes), London: Department of Education and Science.

Ausubel, D. P. (1968) Educational Psychology, a cognitive view, New York: Holt, Rinehart and Winston.

Barnard, T. and Saunders, P. (1994) ‘Is school mathematics in crisis?’, The Guardian, 28 December 1994: 18.

Brown, S. I. (1995) Philosophy of Mathematics Education: POM(E), PO(ME) OR POE(M)?, Philosophy Of Mathematics Education Newsletter No. 8 (May 1995): 16-18. (Located at <http://www.ex.ac.uk/~PErnest/> )

Buerk, D. (1982) An Experience with Some Able Women Who Avoid Mathematics, For the Learning of Mathematics, Vol. 3, No. 2: 19-24.

Buxton, L. (1981) Do You Panic About Maths?, London: Heinemann.

Cockcroft, W. H., Chair, (1982) Mathematics Counts, London: Her Majesty's Stationery Office.

Cooney, T. J. (1988) The Issue of Reform, Mathematics Teacher, Vol. 80: 352-363.

Davis, P. J. (1972) Fidelity in Mathematical Discourse: Is One and One Really Two? American Mathematical Monthly, Vol. 79, No. 3: 252-263.

Davis, P. J. and Hersh, R. (1980) The Mathematical Experience, London: Penguin.

Dowling, P. (1988) The Contextualising of Mathematics: Towards a Theoretical Map, in Harris, M. Ed. Schools, Mathematics and Work, London, Falmer, 1991: 93-120.

Ernest, P. (1988) The Attitudes and Practices of Student Teachers of Primary School Mathematics, in A. Borbas (Ed.) Proceedings of PME-12, Veszprem, Hungary, Vol. 1: 288-295.

Ernest, P. (1989a) The Impact of Beliefs on the Teaching of Mathematics, in Ernest, P. Ed. Mathematics Teaching: The State of the Art, London, Falmer Press, 1989: 249-254.

Ernest, P. (1989b) Mathematics-Related Belief Systems, Poster presented at PME-13, Paris.

Ernest, P. (1991) The Philosophy of Mathematics Education, London: Falmer Press.

Ernest, P. (1994c) The Philosophy of Mathematics and Mathematics Education, in Biehler, R. Scholz, R. W., Straesser, R. and Winkelmann, B. Eds (1994) The Didactics of Mathematics as a Scientific Discipline, Dordrecht: Kluwer: 335-349.

Ernest, P. (1998) Social Constructivism as a Philosophy of Mathematics, Albany, New York: SUNY Press.

Ernest, P. Ed. (1994a) Constructing Mathematical Knowledge: Epistemology and Mathematics Education, London, The Falmer Press.

Ernest, P. Ed. (1994b) Mathematics, Education and Philosophy: An International Perspective, London: Falmer Press.

Gage, N. L. (1989) The Paradigm Wars and Their Aftermath: A 'Historical' Sketch of Research on Teaching Since 1989, Teachers College Record, Vol. 91, No. 2: 135-150.

Gilligan, C. (1982), In a Different Voice, Cambridge, Massachusetts: Harvard University Press.

Glasersfeld, E. von (1983) ‘Learning as a Constructive Activity’, in Bergeron, J. and Herscovics, N. Eds (1983) Proceedings of the 5th PME-NA Conference, Montreal: University of Montreal, Vol. 1: 41-69.

Glasersfeld, E. von (1995) Radical Constructivism: A Way of Knowing and Learning, London: Falmer Press.

Hersh, R. (1979) Some Proposals for Reviving the Philosophy of Mathematics, Advances in Mathematics, Vol. 31: 31-50.

Hoffman, M. (1977) ‘Sex-Differences in Empathy and Related Behaviours’, Psychological Bulletin, Vol. 84: 712-722.

Howson, A. G. (1982) A History of Mathematics Education in England, Cambridge: Cambridge University Press.

Kilpartrick, J and Sierpinska, A., Eds. (1998) Mathematics Education as a Research Domain, Dordrecht: Kluwer.

Lacey, C. (1977) The Socialization of Teachers, London: Methuen.

Lakatos, I. (1976) Proofs and Refutations, Cambridge: Cambridge University Press.

Larrabee, M. J. (1993) An Ethic of Care, London: Routledge.

Lerman, S. (1986) Alternative Views of the Nature of Mathematics and their Possible Influence on the Teaching of Mathematics, unpublished Ph.D. Thesis, King's College, University of London.

Maxwell, J. (1989) ‘Mathephobia’, in Ernest, P. Ed. Mathematics Teaching: The State of the Art, London, Falmer Press, 1989: 221-226.

NCTM (2000) Principles and Standards for School Mathematics, Reston, Virginia: National Council of Teachers of Mathematics.

Riley, R. W. (1998) ‘The State of Mathematics Education: Building a Strong Foundation for the 21st Century’, Conference of American Mathematical Society and Mathematical Association of America, Thursday, January 8, 1998.

Schwab, J. J. (1961) 'Education and the Structure of the Disciplines' in Westbury, I. and Wilkof, N. J., Eds., Science, Curriculum and Liberal Education: Selected Essays of Joseph J. Schwab, University of Chicago Press, Chicago, 1978, 229-272.

Skovsmose, O. (1994) Towards a Philosophy of Critical Mathematics Education, Dordrecht: Kluwer.

Steen, L. A. (1988) The Science of Patterns, Science, Vol. 240, No. 4852: 611-616.

Steiner, H. G. (1987) ‘Philosophical and Epistemological Aspects of Mathematics and their Interaction with Theory and Practice in Mathematics Education’, For the Learning of Mathematics, Vol. 7, No. 1: 7-13.

Thom, R. (1973) Modern mathematics: does it exist? in Howson A. G. Ed. Developments in Mathematical Education, Cambridge: Cambridge University Press: 194-209.

Thompson, A. G. (1984) The Relationship Between Teachers Conceptions of Mathematics and Mathematics Teaching to Instructional Practice, Educational Studies in Mathematics, Vol. 15: 105-127.

Tymoczko, T. Ed. (1986) New Directions in the Philosophy of Mathematics, Boston: Birkhauser.