________________________________________________________________________
PICTORIAL REPRESENTATION AS A MEANS OF GRASPING WORD PROBLEM STRUCTURES
________________________________________________________________
Problem to be solved: Marie and Pavla each had some money but Marie had 10 CZK more than Pavla. Pavla managed to double the amount of money she had and Marie added 20 CZK more to her original amount. They now found that both of them had the same amount. How many crowns did each of them have at the beginning?
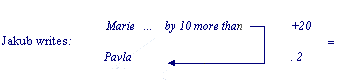
This record of the assignment did not allow him to find a suitable solving strategy. The experimenter recommends him to use the visualisation with the help of line segments, see (Novotn�, Mnichov):
Experimenter (E): Try to record the situation at the beginning.

E: And after the change?
J starts to draw a new line segment.
E: Would not be better to record it in the same schema?
After a short discussion, J's graphical representation is

J: Aha *… I do not need to construct an equation!
This is a small illustration of the power that graphical visualisation brings in the solving process of certain types of word problems.
Pictorial representation (diagrams) is one of the oldest and most used didactical tools for the solving of problems, see e.g. (Volkert, 1989). The importance of pictures, schemes, diagrams etc. grows with the expansion of new technologies such as audio-visual means, hypertext etc.
There are several studies, of which I will list four, analysing the role of figures as a didactical means for improving the learning process in different subject areas. Macek, 1984, Anschauliches Beweisen, 1989, Mares, 1995, Plass et al., 1998.
Mares's paper of 1995 is devoted to learning from pictorial materials. The child's understanding of pictographic materials depends on his/her cognitive structure development. It is connected not only with the age and spontaneous maturation of the child's intellect, but it also depends on the way the child's development is systematically influenced and on the level of thought-provocativeness of the child's environment. Mares characterises the differences between the pre-school and school periods from the point of view of verbal and non-verbal communication:
- In the pre-school period, the verbal and non-verbal communications are well connected. The child usually does not know how to read, his/her reception of knowledge comes from the spoken word and from visual materials (pictures, TV, video etc.).
- In the traditional Czech school education, the verbal and non-verbal communication is gradually disconnected. In schools pupils are taught how to study from a text, but very rarely or not at all how to study from visual materials. When this latter aspect is addressed it is usually restricted to questions concerning the clarity of the material. Questions such as "how to examine a figure?", "according to which rules it was outlined?", "how to draw a figure?" are not taken into consideration.
Mares (p. 319) refers to the term visual literacy which is used in literature in connection with understanding visual materials. It is considered either as an ability to understand ("read") and to use ("create") figures, to think and learn in the terms of figures, or as a set of skills that an individual has to his/her disposal in order to understand visually presented materials and to be able to use it for intentional communication with other individuals.
For Macek, 1984, the figure/diagram is characterised as a partly or completely constructed record. The author uses the term didactical figure for a visual two-dimensional or an audio-visual medium specifically constructed as a means of stimulating and regulating learning activities in the educational process.
The present article is connected with the role of figure in grasping word problem assignments. Some aspects in the specific domain of word problems dealing with the division of a whole into parts have already been presented e.g. in (Novotn�, 1997b), (Novotn�, 1998), (Novotn�, 1999). The theory presented in these articles was supported by the results of experiments with 12-to15-year old Czech students.
We used the stages of word problem solving process presented in (Novotn�, 1997c):
- encoding stage (grasping the assignment),
- transformation stage (transfer to the language of mathematics)
- calculation stage (mathematical solution of the problem),
- storage stage (transfer of mathematical results back into the context).
We will concentrate on the grasping of the assignment and consider only the case when the solver uses a figure.
The following terminology will be used (Novotn�, 1999):
Coding of word problem assignment is the transformation of the word problem text into a suitable system (reference language) in which data, conditions and unknowns can be recorded in a more clearly organised and/or more economical form. The result of this process is a legend. The legend constructed in a pictorial form is called a graphic legend. The reference language contains basic symbols and rules for legend creation.
Note: There exist different reference languages for any one type of word problem. The solver's choice of one of them is influenced by several factors, e.g. by his/her previous experience, preferred information processing style, personal preferences.
Functions of graphical legends
The diagrams - graphical legends can fulfil different roles. We will specify those psycho-didactical functions given in (Mares, 1995), that are relevant for the situation of a graphical legend as a tool of getting insight in the word problem structure.
- Function to represent: Its purpose is to create a solver's adequate mental pictures. The figure is another representation of the assignment problem containing the data, conditions and unknowns of the problem. It can vary from a nearly realistic to a completely schematic drawing.
- Function to organise: Its purpose is to bring a suitable order in a solver's already existing mental pictures and knowledge in order to connect them together. It can perform the passage between process and gestalt during the grasping process.
- Function to interpret: Its purpose is to facilitate the understanding what are the unknowns of the problem and to reveal the most complicated relationships among the facts given in the problem. It helps to eliminate the formation of erroneous mental pictures.
- Function to transform: Its purpose is to influence the solver's information processing by changing the used reference language to another one that is more suitable for the respective solver and to help systematically to recall helpful information stored in his/her memory.
The functions of a graphical legend regarded from the point of view of a solver's emotionality are:
- Function effectively-motivating: Its purpose is to increase solver's positive attitude to the solving of the assigned word problem e.g. by awaking his/her interest in task, by exposing surprising relationships hidden in the assignment, by satisfying the solver's thirst for success.
- Function of concentrating the attention: The figure serves as a means to gain the solver's attention and to concentrate it to the fundamental pieces of information and relationships. (It can occur that a figure suitable from the point of view of its affectively-motivating power can divert the solver's attention in a wrong direction and make his/her grasping of the problem structure even more difficult.)
- Function cognitively-regulating: The graphic legend should be a means for supporting cognitive processes in the solver's grasping of word problems and to highlight the ways to a better interpretation of the facts given in the text.
Specific features of graphic representations
Applying the criteria for the text reception studied in (Gavora, 1991), i.e. passive/active text reception, personal interpretation of the text, use of personal language, we conclude:
- Creation of a graphical legend is an active process, a dialogue between the solver and the text.
- The way of coding the text can be delivered to the solver (by another person, a textbook etc.) or be determined by the solver.
- The solver can use a prescribed way of creating the graphical legend or create his/her own personal reference language.
Pictographic communication differs basically from verbal communication (Macek, 1984) mainly in the following ways:
- A closed set of signs and a conventional language does not exist.
- Usually it is a one-way process without dialogue.
- Generally there is no feedback.
- The danger of distortions or loss of information is rather high whilst subjective factors play an important role.
Information aspects of a graphic legend
The dominant role in the graphical legend creation is played by the teacher more often than when using verbal materials. Therefore the choice of a specific reference language is connected with the concrete group of people - a class, a family etc. In the affective plane, the relationships teacher-student and teacher-class are important. What is very successful in one class can be difficult to understand in another (icons, signs, their position etc. from one reference language can e.g. have completely different meaning in another). This feature of a graphical reference language can be the source of solvers' difficulties.
The following scheme is a modification of the general scheme of the pictographic communication scheme presented in (Macek, 1984) for the case of word problem assignment graphical coding:

Classification of graphical legends according to the impulse for their creation
In our research we identified three legend categories:
- Spontaneous independent figure creation
- Externally managed figure creation
- Creation of a figure in the role of a signal
1. The solver forms his/her graphical legend spontaneously without (or with a minimal use of) a previously learned reference language (Novotn� & Kub�nov�, 1999). The impulse for the legend creation goes out from the solver's internal need to visualise the problem structure.
For the graphical legends classification the following criteria were used:
- shape similarity,
- use of ordinary language and/or mathematical symbols in the legend,
- completeness of the record,
- procedural or conceptual form of the legend.
a) Shape similarity
We use the classification presented in (Macek, 1984).
- Iconic legends consist of real shape record.
- Symbolic legends keep the structural similarity only.
In our experiments (junior secondary level students) the pure iconic spontaneous legend was exceptional. Most students used the reference language consisting of both, iconic and symbolic elements.
Note: Most pupil’s representations are topologically correct rather than iconic.
b) Use of language and/or mathematical elements
In graphical legends reference language, the symbols used are not always pure pictographic ones. Words and/or mathematical symbols are attached. We distinguish two different roles of them:
- Words and separate simple mathematical symbols play the role of an accompanying explanatory means for graphical elements (see e.g. the graphical legend at the beginning of this article).
- During the legend creation, the solver discovers the problem structure and corresponding mathematisation. He/she does not finish the graphical record and uses a partial or complete mathematical representation of the problem.
c) Completeness of the record
The purpose why the solver creates a legend is in most cases his/her attempt to understand clearly and correctly the word problem structure. This grasping consists of several steps (Novotn�, ERCME):
- grasping of objects and identifying those which are relevant to the situation,
- looking for and finding all relationships relevant to the solving process,
- searching for and reaching the unifying view,
- getting the overall insight.
Not all these stages are necessarily recorded in the graphical legend. There are different reasons why the solver does not finish the detailed legend, the most usual are the following ones:
- The solver gains the belief that he/she grasped successfully the problem structure before finishing it (aha-effect), he/she leaves its creation and passes directly to the mathematical processing.
- The solver did not find any relationship of a piece of information and the problem structure.
- The solver finds the creation of a graphical legend too complicated or too time-and/or energy-consuming and therefore records only uncompleted information.
d) Procedural or conceptual graphical legends (Novotn� & Kub�nov�, 1999)
We call a legend:
- procedural when it clearly expresses the process in time, described in the assignment,
- conceptual when all pieces of information are recorded as a whole not showing the changes in time.
2. A model graphical legend for a family of problems is presented to solvers and they form graphical legends using the presented reference language.
The model legend should fulfil the following demands. It should
- manage, regulate and develop the grasping process. The reference language should be as simple and clear as possible not to consume too much of solver's energy when using it,
- activate the solver's mental activity,
- visualise the abstract information from the assignment and enable a creative manipulation with its pictographic elements,
- offer easy orientation in the assignment by a well-organised figure composition and highlight typical features and relationships,
- fulfil by bringing logical and unequivocal interpretation of the recorded information and the need of emotionality by influencing solver's attitudes to the solving of word problems,
- be flexible enough to enable an easy modification for different problems from the family of related word problems, see e.g. line segment legends for the family of word problems dealing with the division of a whole into parts studied in (Novotn�, 1997a).
Creation of a model graphic legend for a family of word problems is always influenced by the author's past experience and personal preferences. It is not necessarily the best one for all other solvers. Therefore it is recommended to present the reference language of the model legend but not to insist on its use at any price. The individual differences usually touches upon the extent of the use of abstract symbols, the use of procedural/conceptual legend type, the composition of the legend and the richness and form of accompanying verbal and/or mathematical labels.
The educational climate and the relationships between the teacher and his/her students play an important role in the acceptance of a model graphical legend by the students. To increase students' creativity and ability to solve modified or non-standard problems, the teacher should not deliver the model legend as a completed algorithm, but construct it in co-operation with the students, let them discover the advantages (disadvantages) of its reference language themselves. In our experiments the usefulness of choosing well presented graphical legends was remarkable especially for weaker students.
3. The ability to solve a certain type of word problems can be increased by facilitating the positive transfer effect (the use of solver's past experience in solving similar problems). A simple figure can serve as a signal to activate the solving schemes stored in the solver's memory.
A typical example is the family of time - distance word problems. It is a difficult task for many students to solve these problems even if they are familiar with the model solutions to similar problems. Simple figures as
![]()
can activate the corresponding algorithm for the correct solving process and help the student to find the solution of the problem.
Conclusions
From the analysis of the graphic legends in solving word problems we find that the passive text reception has no place when creating a pictorial record of the assignment. The solver gives the assignment a new form, his/her personal presentation of the text. He/she adapts the text to his/her abilities and customs.
In the article the positive role of figures in the process of grasping word problem assignment was stressed. The questions of their possible negative influence were not analysed. There exist individual differences in dealing with pictographic materials from the point of view of solver's learning style, ability to draw pictures, influence of the solver's school and/or family background, age etc.
Literature
Gavora, P. (1992). Ziak a text (Student and text). Bratislava, SPN.
Macek, Z. (1984). Obraz jako didakticky prostredek (Figure as a didactical means). Pedagogika, 34, p. 453-467.
Mares, J. (1995). Uceni z obrazoveho materialu (Learning from pictorial material). Pedagogika, 45, p. 319-327.
Novotn�, J. (1997a). Using Geometrical Models and Interviews as Diagnostic Tools to Determine Students‘ Misunderstandings in Mathematics. In: Proceedings SEMT 97. Praha, Prometheus, p. 61-67.
Novotn�, J. (1997b). Geometrical Models in Solving Word Problems That Include the Into Parts (Theory and Practice). In: Proceedings Interakcja teorii i praktyki nauczania matematyki w szkole podstawowej i sredniej. Ed. J. Tocki. VSP Rzesz�w, p. 109-119.
Novotn�, J. (1997c). Phenomena Discovered in the Process of Solving Word Problems. In: Proceedings ERCME 97. Praha, Prometheus, p. 98-102.
Novotn� , J. (1998). Cognitive Mechanisms and Word Equations. In: Beitr�ge zum Mathematikunterricht 1998, Vortr�ge auf 32. Tagung f�r Didaktik der Mathematik vom 2. bis 6.3.1998 in M�nchen. Ed. M. Neubrand. Hildesheim, Berlin, Verlag Franzbecker p. 34-41.
Novotn�, J. - Kub�nov�, M. (1999). Wie beeinflusst eine Visualisierung der Aufgabenstellung den Prozess der L�sung einer Textaufgabe. In: Beitr�ge zum Mathematikunterricht 1999, Vortr�ge auf 33. Tagung f�r Didaktik der Mathematik vom 1. bis 5.3.1999 in Bern. In print.
Novotn� , J. (1999). Analyza reseni slovnich uloh (Analysis of word problem solving process). Praha, Karolinum. In print.
Plass, J.L. & al. (1998). Supporting Visual and Verbal Learning Preferences in a Second-language Multimedia learning Environment. Journal of Educational Psychology, Vol. 90, No. 1, p. 25-36.
Proceedings Anschauliches Beweisen. Eds. K. Kautschitsch - W. Metzler (1989). Schriftenreihe Didaktik der Mathematik, Band 18, H�lder - Pichler - Tempsky, Wien, B.G. Teubner, Stuttgart.
Volkert, K. (1989). Die Bedeutung der Anschauung f�r die Mathematik - historisch und systematisch betrachtet. In: Anschauliches Beweisen. Eds. K. Kautschitsch - W. Metzler. Schriftenreihe Didaktik der Mathematik, Band 18, H�lder - Pichler - Tempsky, Wien, B.G. Teubner, Stuttgart, p. 9-31.
Jarmila Novotn�
Charles University
Faculty of Education
M.D.Rettigove 4
116 39 Praha 1
The Czech Republic
Tel.: +420-2-21900251
E-mail: jarmila.novotna@pedf.cuni.cz
Acknowledgement: The research was supported by the projects GACR No. 406/99/1696 and GAUK 306/1998/A.