_________________________________________________________________________________
THE STRUCTURE OF TRIADS AND PILOT EXPERIMENTS
________________________________________________________________
1. Introduction
This paper is focuses on a part of my research. I am interested in the thinking processes involved in solving the mathematical tasks which I have given to 10-11 year old pupils in the United Kingdom. The tasks have a common "element", the triad. I define a triad as three ordered natural numbers (excluding zero) with the third number being the sum of the first two numbers. The tasks with triads were chosen from [9].
The reason why these tasks were chosen is that the tasks are non-standard and therefore the pupils carrying out the tasks cannot use school stereotype answers. A procedure was given to the pupils to generate further triads, the resulting structure produced a pattern. Looking for pattern is the first stage of generalisation which is a part of and an outcome of human thinking. The tasks using the triads are difficult to grasp without a concept of order and an ability in mental arithmetic, which is also a wide field of the research. In addition the structure of triads is a combinatorial structure because they create a tree-graph that appears in many combinatorial and as well as non-combinatorial problems. Finally experience shows that if a task is interesting for pupils they enjoy carrying out the task and discussing it. I found that the tasks I devised with triads answered this purpose.
The 10 to 11 year age group was chosen for the following reasons: It was thought that the level of mathematics needed for the tasks was most appropriate for the average ability of this age group. This age group of pupils moves from Primary to Secondary education at the end of the academic year. A major implication of this is that they move from being taught by generalist teachers for their mathematics in the primary school to specialist teachers of mathematics in the secondary school. We ask ourselves what thinking mechanisms the pupils use before they move to Secondary education.
2. Pilot experiments
The pilot experiments were carried out in a primary school in Derby in the United Kingdom in April and May. Three pilot experiments were done in a quiet library where the experimenter was with three 10-11 year old pupils usually from 9.30 a.m. to 12.00 a.m. The experimenter asked their teacher to choose pupils with average ability for the experiment. Discussion during the tasks was recorded on tape.
2.1. The way of giving the tasks in the pilot experiments
Phase (i) - Introducing the definition of the triad to the pupil:
� Experimenter’s description of a triad – "A triad means three natural numbers (excluding zero), the first two numbers are any numbers, e.g. 9, 6 or 8, 11 or 5, 5. We get the third number by adding together the first two numbers".
� Experimenter gives examples of the triads (e.g. (9,6,15), (8,11,19), (5,5,10)).
� Experimenter gives tasks to the pupil: The first two numbers of the triad are: (3,8, -). The third number is missing. Fill in the number in the third place. The pupil fills in the number.
What is the third number of the following triads (7,5,_), (17,23,_)? The pupil fills in the numbers.
Is the triplet (7,8,12) a triad? The pupil answers the question.
Show why the triplet is not a triad. The pupil shows it.
Phase (ii) - Introducing a procedure to the pupil:
� The experimenter takes a sheet of paper and writes the triad (1,5,6) on line 1. Then the experimenter gives the following procedure:
We put the triad (1,5,6) on line 1. Then we go to line 2 and we get two triads in this way:
- We take the first number of the triad on line 1, i.e. 1 and put that number in the first place of the new triad on line 2.
- Then we take the second number of the triad on line 1, i.e. 5 and put the number in the first place of the second new triad on line 2.
- Two extracts of the pilot experiments
- Experience gained from the pilot experiments
- Making the third term of the new triad by adding up the first and second terms of the new triad.
- Then we take the third number of the triad on line 1, i.e. 6 and we put that number in the second place of the new triad on line 2.
- Then we add up the first two numbers of the new triad and we get the third number (7) of the first triad on line 2.
- We then take the third number of the triad on line 1, i.e. 6 and put the number in the second place of the new triad on line 2.
- Then we add up the first two numbers of the new triad and we get the third number (11) of the second triad on line 2.
The end point of this phase of the work, i.e. the work the experimenter with the pupil, is Fig. 1a or Fig. 1b. (See Fig. 1a, 1b)
Fig. 1a*
1………………………………………..…(1,5,6)………………………………………….
2………………..…(1,6,7)……………………………...……….(5,6,11)…………………
Fig. 1b*
2………………..…(1,6,7)……………………………...……….(5,6,11)…………………
1………………………………………..…(1,5,6)………………………………………….
Phase (iii) - The experimenter introduces the tasks to the pupil:
� What will the triads on line 3 look like? What will the triads on line 4 look like?
� How many triads do you think there will be on line 3, 4, …, 10?
*In some experiments the line 1 was given up on the paper (Fig. 1a) and in some experiments the line 2 was given down on the paper (Fig. 1b).
� Find the ‘smallest’ triad on line 10. The smallest triad on a line is the triad that has the smallest sum. We get the sum of a triad if we add up the three numbers that make up the triad.
Before you start looking for the smallest triad on line 10 which of the triads (2,5,7) and (3,8,11) is smaller?
� Find the ‘biggest’ triad on line 10. The biggest triad on a line is the triad, which has the biggest sum.
Before you start looking for the biggest triad on line 10 which of the triads (4,6,10) and (5,9,14) is bigger?
(Carrying out and discussing the tasks by the pupils follow.)
The first extract from experiment 2:
Place: Bishop Lonsdale C. of E. (Aided) School, the library, Derby, UK
Date: 29. 4. 1998
Time: 9.30 – 11.45 a.m.
Pupils: Ben – aged 10 (boy), Stephen – aged 10 (boy), Georgina – aged 10 (girl)
Teacher’s evaluation: Ben, Stephen, Georgina – average ability
Note: Georgina has a new piece of squared paper. She has written the triad on line 1 and then the triads (1,5,7), (5,6,11) on line 2.
Exp. 51: We’ve said we take the first and the third number of the triad on line 1.
Note: The experimenter works with the boys. (2 minutes)
Note: Georgina has corrected the third number that is right. She has written the triad (1,5,6) on line 2 and the triads (1,6,7), (5,6,11), (6,11,17) and (5,11,16).
Exp. 55: Could you have the same triads on two lines? (Pause 10 seconds.)
Exp. 56: What is the first number of the triad on line 1?
Georgina 09: 1. (The experimenter writes the number above the triad on line 2.)
Exp. 57: What is the third number of the triad on line 1?
Georgina 10: 6. (The experimenter writes the number above the triad on line 2.)
Exp. 58: So what is the third number of the triad on line 2?
Georgina 11: 7. (The experimenter writes the number above the triad on line 2.)
Exp. 59: Very good. Take the second number and the third number of the triad on line 1.
Georgina 12: 5 and 6.
Exp. 60: Have you had the triad that has the first number and second number 5 and 6?
Georgina 13: Yes.
Exp. 61: Very good. Try to continue from the line 2.
Note: The experimenter works with the boys. (4 minutes)
Note: Georgina has written the triads (6,7,13), (1,7,8), (5,11), (6,11), (6,17), (5,16) and (6,17) again.
Exp. 73: Each triad has three numbers. (Pause 10 seconds.)
Exp. 74: What do we do with the first two numbers? (Pause 30 seconds.)
Exp. 75: We must add them up. The sum of these numbers is the third number. (Pause 40 seconds.)
Exp. 76: Is (5,11) the right triad?
Georgina 14: 16.
Note: She writes 16 in the triad.
The second extract from experiment 3:
Place: Bishop Lonsdale C. of E. (Aided) School, the library, Derby, UK
Date: 22. 5. 1998
Time: 10.00 – 12.00 a.m.
Pupils: Klaine – aged 10 (boy), Mathew – aged 10 (boy), Claudia – aged 10 (girl)
Teacher’s evaluation: Klaine, Claudia – average ability, Mathew – below average
ability
Experimenter 40: Could you tell me what we get from the triad (1,6,7)?
Klaine 13: 1, 6. (Pause 20 seconds.)
Exp. 41: The one is (1,7,8). But we can get another triad from the triad (1,6,7).
Mathew 15: The triad is …
Exp. 42: Think, Klaine. (Pause 30 seconds.)
Exp. 43: We’ve said that we take the first number and the third number that’s the triad (1,7,8). Then we take the second number and the third number that’s another triad. Listen, we need the second number and the third number that are?
Mathew 16: 13.
Exp. 44: Yes. It is 13 together. But the triad is? (Pause 10 seconds.)
Exp. 45: The triad is (6,7,13). Klaine, please write the triad down on line 3. (6,6,12) is not the right triad. Note: Klaine has written (1,7,8), (11,5,16), (6,6,12), (11,11,22), (6,7,13).
Exp. 46: You have from the triad (1,6,7) on line 2 the triads (1,7,8) and (6,7,13) on line 3. Very good. How did you get the triad (11,5,16)?
Klaine 14: 11+5 is 16.
The pilot experiments were based on the experimenter’s ideas about the way pupils think. However, these ideas did not conform to reality. It was thought that the tasks: What do the triads on line 3 look like? What do the triads on line 4 look like? would be easier than the other tasks and that the focus of difficulties would be in the tasks: Find the smallest triad on line 10. Find the biggest triad on line 10. The answer to the question ‘what do the triads on line 3 or 4 look like?’ requires a knowledge and understanding of the procedure and an ability to follow it. The task to find the smallest triad on line 10 is based on finding the smallest triads on the first four or five lines, finding a pattern and applying the pattern to find the smallest triad on line 10. It was assumed that if the experimenter explained the procedure to the pupils they would be able to follow it. The reality was different. (See examples above.) The focus of difficulties was in the procedure. If the pupils were able to follow the procedure they were mostly able to carry out the other tasks.
There were situations that the experimenter had not expected and therefore the experimenter had not been able to react to the situations. For example, the pupils did not understand the task even after several explanations or their answer to an ‘easy’ question (in the experimenter’s opinion) was not right. It is supposed that it is possible to affront these situations (The other experiments have affirmed it.). For instance, pre-prepared experimenter’s reactions might help the experimenter to be able to use them readily during experiments with the aim to find how the pupils think and not to teach them. But to have pre-prepared reactions does not always mean that the experimenter knows how to react to the situations which arise during experiments. Even though the experimenter has the pre-prepared reactions to the situations it can happen that the experimenter does not always react readily and/or appropriately.
The pilot experiments showed a need to systematise the process of the experiment. A sequence of logical steps was prepared, which it was hoped would help the experimenter as the researcher. In the case of triads the experimenter needs to find out first whether the pupil understands the concept of a triad. Only then can one begin an explanation of the procedure. It is necessary for the experimenter to make sure of the pupil’s understanding of the procedure. After giving another task it is possible to find out by appropriate questioning whether the pupil understands the task. It is hoped that systematised experiments (consisting of logical steps) enables good evidence about the pupil’s solving process to be obtained. However, it must be remembered that if the pupil does not know what a triad means, it is impossible to say anything about the pupil’s concept of order and addition either.
It is thought that not only the systematised experiment but also the standardisation of the experiment might help the experimenter. If the experiment is standardised, it eliminates as many variables as possible. The variables are for example: the number of the pupils in a group for the experiment, the experimenter’s formulation of the tasks and their order, the choice of the experimenter’s questions for the pupils performing the task. By standardisation of the experiment it is hoped that all pupils perform the tasks under similar conditions which will help the experimenter to do comparative analysis and to analyse deeply pupil’s work.
3. The structure of triads
3.1. The concept of triads
In order to understand the structure of triads it is necessary to define what a triad is. Definition: N is supposed to be without zero. An element (a,b,c) of a subset of the Cartesian product N x N x N is said to be a triad if c=a+b.
The triad according the definition means that one of the following situation can happen: a< b, a=b, a>b, but a+b is always in the third place. If a� b then the triads (a,b,a+b) and (b,a,a+b) are different. If a=b then the triads on line 2 made from the triad (a,b,a+b) on line 1 look identical; that is such a triad on line 1 could be represented as (a,a,2a) which leads to the identical triads (a,2a,3a) and (a,2a,3a) on line 2. The both triads on line 2 will produce the same structures and therefore to work with one structure is sufficient. (For the difference see Fig. 2 and Fig. 3)
Fig. 2
1………………………………………...(a,b,(a+b))…...…………………………………..
2……………...(a,(a+b),(2a+b))………...…………………(b,(a+b),(a+2b))……………..
3. (a,(2a+b),(3a+b))((a+b),(2a+b),(3a+2b))…((b,(a+2b),(a+3b))((a+b),(a+2b),(2a+3b)).
Fig. 3
1……………………………………….…..(a,a,2a)…...…………………………………...
2………………….(a,2a,3a)………...………………………….(a,2a,3a)……..………….
3………(a,3a,4a)……………(2a,3a,5a)……………(a,3a,4a)…………..(2a,3a,5a)……..
3.2. The concept of order in two contexts
The procedure requires the knowledge of order in two contexts.
The first context is based on the fact that a triad (a,b,a+b) consists of three terms, the first term is a, the second term is b and the third term is a+b. All three terms of a triad are in a specific order which is important for the rest of the procedure.
The second context is based on following the procedure in the pupils’ heads. The following description how the pupils follow the procedure might be:
The first triad on line 2 is formed by:
1. Taking the first term of the triad on line 1 and making the first term of the new triad,
2. Taking the third term of the triad on line 1 and making the second term of the new triad,
3. Making the third term of the new triad by adding up the first and second terms of the new triad.
The second triad on line 2 is formed by:
1. Taking the second term of the triad on line 1 and making the first term of the new triad,
2. Taking the third term of the triad on line 1 and making the second term of the new triad,
Bold ordinal numbers express the second context of the order. (See Fig. 4)
Fig. 4
1………………………………………...(a,b,(a+b))…...…………………………………..
2……………...(a,(a+b),(2a+b))………...…………………(b,(a+b),(a+2b))……………..
We speak about the first and second and third term of a triad but we also speak about the first triad and second triad and later on about the third and fourth triad on line 3 and so on. We can distinguish between the different contexts of order by looking at the connection of an ordinal number and the word that goes after it. For example, a pupil might say ‘I put the second number of the triad there’ (the first context), or ‘I have already written down the second triad on this line’ (the second context). If new triads on line 3 are made, the pupil needs to think of the two triads on line 2 separately and repeat the previous procedure for each of them. From this point of view the pupils meet a multiplicity of orders and the real need for the concept of order is evident.
3.3. The concept of addition
Addition has three components when applied to the teaching of it to children: concept and skill acquisition and application. (Skill acquisition is when a pupil has an ability to perform a task which might be to recall and use an algorithm correctly for example, or to put numbers into a formula and do the necessary calculations.) Addition is a concept because it is necessary for pupils to understand what is meant by "add this number to that number". One of the simplest ways of defining addition without using numbers is that addition is the putting together of two groups of objects and finding the cardinal number for the totality of the two groups. It is also necessary to interpret and understand not only one but all the many ways in which addition can be expressed. For instance one way is 3 + 4 =, and another ‘what is the sum of three and four’. Addition requires a skill. This means an ability to undertake an algorithm which "performs" the process of addition. This skill needs a complete understanding of the concept of place value as soon as the summation is greater than 9. (See Fig. 5. David does not have the concept of place value and treats the sum as two separate columns of digits.) Using constructivist teaching techniques to give the pupils both understanding and skill, allows the pupils to apply their knowledge in very different situations. If pupils get only one component of addition (mentioned above), for example skill (the process form), then this is formalist teaching in the extreme and can be expressed as – "Addition is the process that must be follow to get the right answer."
Fig. 5
David (9years-old pupil):
![]()
There is a rising difficulty of addition involved in following the procedure. At the beginning of the procedure the addition is relatively easy, depending on the initial numbers of the triad on line 1. The answers to the first task - ‘what do the triads on line 3 look like?’ given the triad on line 1 is (1, 5, 6), are four different triads. In one case only the pupils do have to add over ten. To get the third term in each of the triads on line 4 is more difficult than to add the numbers on line 3, because in four cases the sums of the first two terms is over twenty. From the addition of number point of view the task to find the biggest triad on line 10 is the most difficult. As the pupil’s procedure develops from one line to the next line and the biggest triad on each line has the biggest numbers on the line the addition becomes increasingly difficult.
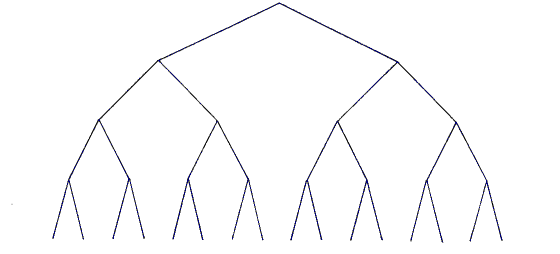
3.4. The structure of triads as objects
The structure of the triads is a branching one like a tree (See Fig.6, see next page.). Each triad produces other two triads that have their own position within the combinatorial structure. There are two aspects of order already mentioned above, one, which relates to the order within the triad and the second which, relates to the order within the procedure. The second aspect of the order defines the combinatorial structure. This dual ordinality makes the undertaking of the whole structure for children both difficult to achieve and even more difficult to visualise.
Fig. 6
4. Analysis of three pilot experiments
4.1. Case 1 - Ben (understanding of the combinatorial structure and misunderstanding of the procedure)
Extract from experiment 2
Place: Bishop Lonsdale C. of E. (Aided) School, the library, Derby, UK
Date: 29. 4. 1998
Time: 9.30 – 11.45 a.m.
Pupils: Ben – aged 10 (boy), Stephen – aged 10 (boy), Georgina – aged 10 (girl)
Teacher’s evaluation: Ben, Stephen, Georgina – average ability
See Fig. 7 Case Ben
Ben makes this figure on his own without discussion with the experimenter.
Ben is not given a full explanation of the activity because the experimenter thinks that he understands what to do. He starts carrying out the task in his creative way (See Fig. 7.).
When an experimenter gives a task to a pupil it usually creates some activity from the pupil. It is always thought that the pupil’s activity is deterministic that means the activity is prescriptive and the pupil has no opportunity to use his/her own initiative. But the reality is different. It might happen that the activity is not explained to the pupil clearly, the task itself is not clear, the pupil does not understand the task, the activity is not prescriptive clearly and the pupil can use his/her own initiative. There are at least two different scenarios. The first one is that the activity is explained clearly, the task is clear. However there is the thought fixed in the pupils’ head that there is no space for creative work. Then
Fig. 7 Case Ben
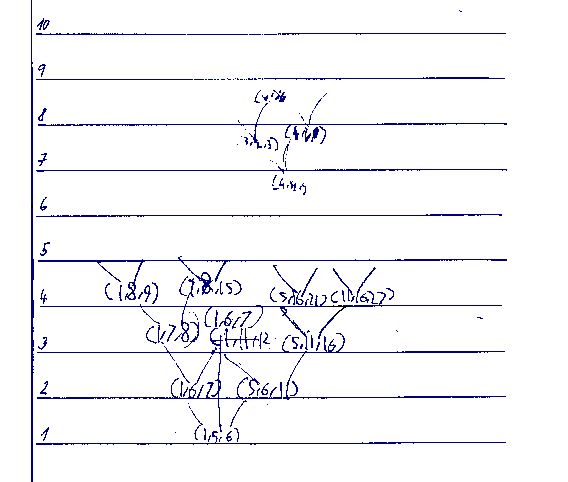
the pupil’s problem is how to carry out the experiment with the idea that everything that is given to him/her is prescribed. But this is not how we wish the pupils to work. The second scenario is that the activity is roughly sketched because the experimenter thinks that such explanation is sufficient.
This research is focused on the second kind of scenario which took place during the pilot experiments. It was thought that the experiment would be prescriptive but reality showed that there were two ways how the pupils worked with the given tasks:
- the deterministic way,
- the creative way.
- The pupil understands the task and he/she prescriptively carries out the task without problems or the pupil realises that he/she does not understand how to find the new triads and therefore the pupil insists on the experimenter re-defining the task.
2. The pupil does not fully understand the task but he/she fills in the triads in his/her creative way. The pupil wants to find the triads. He/she tries to find some strategy. The experiments in the United Kingdom show in many cases that if the pupils do not fully understand the task the pupils do not follow the instructions exactly and work creatively. (One such case is the experiment with Ben.). This probably means that pupils in the United Kingdom are often open-minded about the tasks they are given and are allowed the flexibility to create their own methods of solutions.
The experiment raises the following questions:
When does Ben write the triad (1,11,12) on the line 3? In what order are the triads written? Why is (1, 6, 7) written as the central triad on line 3? Why is this triad joined with the triads on line 2? Is the triad (1,11,12) joined to the triad on line 1 or is the new triad (1,6,7) joined with the triad on line 1 later? How are the numbers in the triad (1,11,12) found?
One possibility is that 1 is the first number of the first triad on line 2, 11 is the third number of the second triad on line 2, 12 is the sum of 1 and 11. The second possibility (less probable) is that 1 is the first number of the triad on line 1 and 11 is the sum of the second and the third number of the triad on line 1. Then 12 is the sum of 1 and 11. The triad is sound in that Ben realises that to get the third term he must add the first and second term that is 1 + 11 is 12. Only one thing is not fully clear, how has he got the 11?
Considering the analysis from another point of view. It is mentioned above that the structure of triads is combinatorial. The lines of the branches going from the triads on lines 1 and 2 are not clear. (See Fig. 7) The branches going from the triads on line 2 are right in that two branches come from each triad on line 2 to line 3. It could be that because he drew the branches from line 2 and the middle ones met on line 3 he thought he should only have one triad and so became confused. There are no branches going from this ‘middle term’ on line 3 to line 4 because the triad is crossed out. Ben has made the new triad (1,6,7). There are not any branches probably because of the reason of the hampering factor that the triad (1,11,12) does not belong to the structure and the triad (1,6,7) is already written but in different position than the triad (1,11,12) and there is no place for any branches. The branches going from the outer two triads on line 4 are clear and correct as are the triads. Each triad on line 4 has the two branches. The pairs of branches on line 4 are qualitatively the same as he had drawn from line 2. There is not a ‘hampering’ factor on line 4 as on line 3. The branches on line 3 are different. By drawing the branches on line 4 Ben is already indicating that he knows the procedure such that each triad produces two triads on the following line. Ben might tell himself that he would continue in this way. The branches going from triads mean only that bifurcation occurs. In this case the branches do not mean relationship between the triad and its next triad made on the following line. At this moment the pupil has got an insight into the structure and the task concerning the number of triads on each line could be less difficult than if the pupils has not got an insight into the structure. The problem of how to make the triads on a certain line still remains.
4.2. Case 2 - Stephen (incompetent transfer of one pattern in one situation to another situation)
Extract from experiment 2:
Place: Bishop Lonsdale C. of E. (Aided) School, the library, Derby, UK
Date: 29. 4. 1998
Time: 9.30 – 11.45 a.m.
Pupils: Ben – aged 10 (boy), Stephen – aged 10 (boy), Georgina – aged 10 (girl)
Teacher’s evaluation: Ben, Stephen, Georgina – average ability
Stephen completed the figures shown below and discussed his work with the experimenter. The analysis of the experiment is focussed on two tasks:
- Find the biggest triad on line 10 (the triad (1,5,6) on line 1). (See Fig. 8)
- Find the smallest triad on line 10 (the triad (2,5,7) on line 1). (See Fig. 9)
Comparing Stephen’s work with the other pupils in his group, he is very quick with his work and so he had time to attempt the extra task.
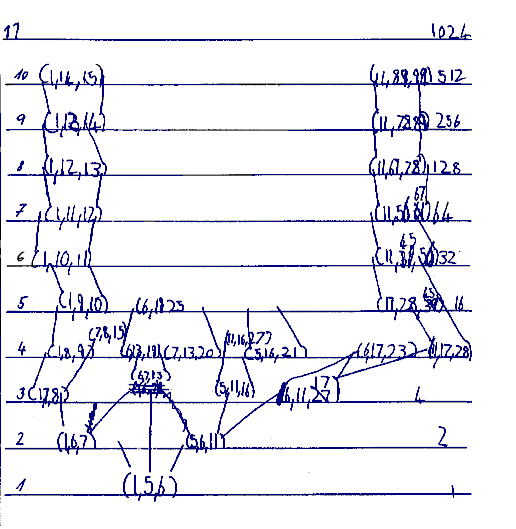
See Fig. 8 Case Stephen
The first task
Stephen has found the smallest triad on line 10 without any problem. To find the biggest triad on lines 1, 2, 3, 4 is not difficult for him because there are all triads on these lines. He can compare the triads easily. Stephen has not written all triads on line 5. He has only the smallest triad (1,9,10) and the triad (6,19,25) which is the smallest triad following from the second triad on line 3. From the last experience (finding the smallest triad) he knows that he does not need to write all triads down on line 5. Stephen knows that the biggest triad on line 4 is (11,17,28). He takes the first and the third number of the triad (11,17,28) and makes the new triad (11,28,39). This triad is the "biggest" triad on line 5 for him. He uses the same pattern as in the case of finding the smallest triad. By this way he constructs the other "biggest" triads on lines 6, 7, 8, 9 and 10. Then the experimenter asks him if the triad (11,28,39) is the "biggest" triad on line 5. The experimenter says that she knows a bigger one. Stephen discovers a bigger triad (17,28,45) on line 5. Then he corrects only the second number of his "biggest" triad on line 6. This gives the triad (11,45,56). Similarly he always corrects the second number only and then the third number as the sum. From this it is obvious that discovering the pattern for finding the smallest triad had such a strong influence on Stephen that he wants to use it once more for finding the biggest triad.
The wording of the tasks: Find the smallest triad on line 10 and find the biggest triad on line 10 is nearly same. There are two words: smallest and biggest that look dual in the task but the patterns are completely different and therefore the outcomes are different. (Stephen takes the task to find the biggest triad on line 10 as the analogical task to the task to find the smallest triad on line 10.)
See Fig. 9 Case Stephen
The second task
Stephen worked on the procedure without any problems and so the experimenter gave him the task: ‘Find the smallest triad on line 10’. He finds the smallest triads on lines 1, 2, 3, 4 and 5 without difficulties. Then he jumps to line 10 and he writes the triad (4,26,30) as the smallest triad on line 10. Stephen multiplies the numbers 2, 13 and 15 by two. Why does he multiply the numbers by two? There are two possible answers to this. Firstly the number two could have connection with the numbers of lines. The smallest triad (2,13,15) is on line 5 and the task is to find the smallest triad on line 10 (5.2=10). This is the transfer of one multiplication by two to another multiplication
Fig. 8 Case Stephen
by two. The second possible answer is that the pattern that arises from the combinatorial structure is transferred to the triads. Stephen saw the pattern when he carried out the task: ‘How many triads do you have on line 3, 4, …, 10?’ He discovered very quickly that the number of triads on each line is a double of the number of triads on the previous line. This experience is so strong that this doubling is transferred to the numbers of the smallest triad.
Fig. 9 Case Stephen

After Stephen had found his version of the smallest triad (4,26,30) the experimenter pointed to the first number 2 in the smallest triads on line 1, 2, 3, 4 and 5. Stephen was then asked why there was not the number 2 in the triad on line 10 if the number 2 is repeated in each smallest triad on the first five lines. Stephen crossed out the number 4 on line 10. He then looked at the pattern of the second term in the triads on lines 1, 2, 3, 4, 5 and saw these were increasing by 2 and counting on quickly found that the second term on the smallest triad on line 10 was 23 (a new interpretation). Then he wrote the triad (2,23,25) on line 10. Why did Stephen correct the smallest triad on line 10 so quickly? When the experimenter questioned him he was not sure of his original pattern. Stephen rejected this pattern because he found another pattern which made more sense to him.
Something similar happens when a pupil carries out a combinatorial problem. The pupil knows that variation or combination should be used for carrying out the problem. He/she uses the variation. The pupil’s teacher shakes his/her head. That means that the teacher rejects the variation. The pupil crosses out the variation and uses the combination.
Because Stephen corrected the triad on line 10 so quickly it is thought that he has the two patterns at the same time: the combinatorial pattern and the triad pattern. It seems that the combinatorial pattern is activated strongly but at the moment when the experimenter raises doubts about it Stephen immediately uses the triad pattern.
Comparing the United Kingdom and the Czech Republic our experiences show that looking for patterns is used considerably in the United Kingdom to develop pupils understanding of mathematics. Pupils are asked to look for relationships (‘patterns’), to extend series such as the ‘square numbers’ or to find the relationship which exists in a set of co-ordinates. What do we mean by a pattern? Elementary pupils begin with actual patterns – counting in twos with materials, later square numbers, triangular numbers and then series. Then the patterns make schemes in a pupil’s head. The scheme is a universal model. At the beginning the pupil has separate models, e.g. 3+2=2+3, 3+1=1+3, 2+5=5+2. Then the pupil makes the scheme a+b=b+a. The pupil knows that if he/she swaps places of the numbers a and b (b+a) that the result of addition is same as before (a+b). It is the universal model. The universal model should be the product of separate models. Making the universal model should be accompanied with feedback. According to our experiences pupils in the United Kingdom do not go back to the separate models. The pupil may find a different pattern than what it should be and then he/she finishes the task using that pattern (See Fig. 8). Or the pupil can have several patterns in his/her mind and then he/she chooses one that is appropriate according to his/her opinion (See Fig. 9).
4.3. Case 3 - Jessica (the use of a different symbolism)
Extract from experiment 1:
Place: Bishop Lonsdale C. of E. (Aided) School, the library, Derby, UK
Date: 27. 4. 1998
Time: 9.30 – 11.30 a.m.
Pupils: Adam – aged 10 (boy), Andrew – aged 11 (boy), Jessica – aged 10 (girl)
Teacher’s evaluation: Adam, Andrew and Jessica – average ability
Jessica’s working is shown below. She discussed her work with the experimenter.
Fig. 10 Case Jessica (See next page.)
Jessica followed the procedure without difficulty. She finds all the triads on lines 1, 2, 3 and 4. Then she writes these pairs on line 5: (10,17), (22,23), (25,32), (27,33), (26,37), (38,41), (29,40), (39,45). (See Fig. 10). The ordered pair (10,17) is made from the triad (1,8,9) on the previous line in
Fig. 10 Case Jessica

the following way: 1+9=10 and 8+9=17. Each of the pairs is made in the same way that is she has written down the third term of each of the pair of terms formed from the triad on the previous line. The experimenter observed her working and asked her how many numbers she should have in her triad, pointing to the pair (10,17). Jessica answered that it had only two numbers and the "triad" (10,17) was not real triad.
Why did Jessica write the pairs on line 5? She saw that there were already many triads on line 4 and therefore there will be more triads on line 5 than on line 4. She probably realized that on line 10 there would be many more triads than on line 5. So Jessica simplified the record of triads because she wanted to save time and space. She foresaw the problem that she would not have space to write down the triads on line 5 or on succeeding lines and that is why she looked for a different way to record the triads. She worked in creative way. The pairs of triads are written down as the pair of numbers, e.g. (1,8,9) and (8,9,17) become (10,17). Jessica determines a new objective and discovers and uses a new symbolism.
A mathematician would use different brackets for the object, e.g. [10,17] in order to distinguish two different objects: the triad and the pair. The mathematician would not say that the "triad" (10,17) is not a real triad as Jessica says. The mathematician would say that it is a new symbol that means a pair of triads. Jessica is not ready to understand this subtly at this stage.
When Jessica was given the task: ‘Find the smallest triads on line 10’ she had a problem. She found the smallest triads on lines 1, 2, 3, 4 without difficulties but she had a problem to find the smallest triad on lines 5 and 6. She did not know how to continue. Jessica broke the ‘pair’ (10,17) down into the triads (1,9,10) and (8,9,17). She then wrote down the pair (11,19) on line 6. That pair represented the two triads (1,10,11) and (9,10,19) on line 6. Then she crossed out the pair, wrote down the number 11 again, then she crossed out the number 11. Finally she wrote down the triad (1,10,11) as the smallest triad on line 6. She then wrote the number 12 on line 7. This number represented the triad (1,11,12) as the smallest triad on line 7. She crossed out the number 12 and wrote down the triad (1,11,12).
Her way of finding the smallest triads on lines 5 and 6 shows that her origin thought about the way of recording the triads has been a great experience. The new symbolism does not disjoin from the origin concept of a triad. Jessica is able to cross from one type of symbolism to another type whenever she feels it necessary.
5. Conclusion
The paper focuses on the initial part of our research and is divided into two parts. The first part of this paper describes our methodology for the pilot experiments, our experimental experiences and our didactical view of the mathematical structure with which the 10-11years old pupils work. The second part deals with an analysis of the three pilot experiments. The order of the chapters follows almost what happened in reality (the way the real research proceeded) but there are some differences. The first part of the research corresponds with the first two chapters of the paper (1., 2., 2.1). As soon as it was known what the vehicle would be on which the research would be based it was necessary to determine a procedure and a logical mathematical development within the experiment. This was based on the experimenter’s thoughts of how the pupils would approach the work.
The second part of the paper concerns the experimenter carrying out pilot experiments and then analysing them (2.2, 4.1, 4.2, 4.3). This gave valuable insights into how the pupils would react to the tasks, the procedure and the mathematical order of the tasks. These experiences enabled the experimenter to look at the experiment from the didactical point of view (2.2, 2.3, 3.1, 3.2, 3.3, 3.4).
The importance of the pilot study was that it showed that the experimenter’s original thoughts on how the children would respond to the work were not completely correct. It was found that it was necessary to modify the procedure, the order of some of the questions, the language used in the experiment and the way in which the work was presented to the pupil. These changes should allow the pupil to follow the procedure more easily, understand the work better and the experiment. These changes should allow the experimenter to express more explicit and clearer guidance and questions for the pupils than before. One other important factor which these changes brought about was to bring a standard form to all the procedures, the tasks, the order and the way of questioning. This meant that the experiment could be carried out in any school in any country and all the pupils would have exactly the same experience. These changes to the experiment will enable us to standardise the work and thus allow us to analyse the results more thoroughly and comparatively.
The modified experiments were then given to 10 to 11 year old pupils in three Schools in the United Kingdom. In the near future the modified experiments will be given to pupils of the same age group in the Czech Republic. The standardisation of the experiments will then allow an analytical comparison of the pupils` approaches and performance in the tasks between the pupils in the United Kingdom and the Czech Republic.
References:
[1] Ciosek, M. (1995). O roli przyklad�w w badaniu matematycznym. Dydaktyka matematyki, 17, p. 5-85.
[2] Ernest, P. (1997). Mathematical activity and rhetoric: A semiotic analysis of an episode of mathematical activity. In: Philosophy of mathematics education journal 10 (1997). Ed. Ernest, P., University of Exeter, http://www.ex.ac.uk/~Pernest/, UK.
[3] Hejn�, M. a kol. (1990). Te�ria vyucovania matematiky 2, SPN Bratislava, SR.
[4] Hejn�, M. – Stehl�kov�, N. (1998). Tri�dy – n�stroj modelov�n�. In: Sborn�k Dva dny s didaktikou matematiky 1998. Ed.: Jirotkov�, D. – Stehl�kov�, N., p. 36-40, PedFUK Praha, CR.
[5] Kratochv�lov�, J. (1998). Tri�dy jako n�stroj v�zkumu myšlenkov�ch procesu pri rešen� probl�mu. In: 6. setk�n� ucitelu matematiky všech typu a stupnu škol. Ed.: Ausbergerov�, M. – Novotn�, J., p. 119 – 126, Mari�nsk� L�zne, 21. – 23. r�jen 1998, CR.
[6] Littler, G.H. et al. (1995). Introduction to Number , University of Derby, UK.
[7] Littler, G. H. et al (1995/6). Place Value Bks 1, 2, 3. University of Derby, UK.
[8] Novotn�, J. (1998). Cognitive Mechanismus and Word Equations. In: Beitr�ge zum Mathematikumterricht 1998, Votr�ge auf 32. Tagung f�r Didaktik der Mathematik vom 2. bis 6. 3. 1998 in M�nchen. Ed. M. Neubrand. P., p. 34-41, Hildesheim, Berlin, Verlag Franzbecker, CR.
[9] Rep�š, V. – Cernek, P. – Pytlov�, Z. – Vojtela, I. (1997). Matematika pre 5. rocn�k z�kladn�ch škol. Prirodzen� c�sla. Orbis Pictus Istropolitana ISBN Bratislava, p. 4, SR.
Jana Kratochv�lov�
Charles University
Faculty of Education
M.D.Rettigove 4
116 39 Praha 1
The Czech Republic
Tel.: +420-2-21900176
E-mail: jana.kratochvilova@pedf.cuni.cz
Acknowledgement: The research was supported by the project GAUK 306/1998/A.