![]() ______________________________________________________________________________________
______________________________________________________________________________________
TEACHERS AS RESEARCHERS: THE BEAR PROBLEM
Thomas C. O’Brien and colleagues
_____________________________________________________________
Susie Bargiel
Kathy Feely
Linda Gwyn
David Hoffman
Carol Kaplan
Carolyn Myers
Thomas C. O’Brien
Lee Scissors
Sharon Steinberg
Davi Turman
Jan Wilson
Susan Wise
Introduction Thomas C. O’Brien
Suppose you ask a five year old child, "What is 9 + 9?" And suppose the child answers, "19." What do you know? What would you do? There are many things you could do. One thing you could do is to find out how the child got the 19. The adult who had asked the child the original question knew that it was important to find out what the child was thinking.
"How did you get the 19?"
"Well," said the child patiently to what was plainly a dim-witted adult, "You asked me about 9 + 9. And I knew that 10 + 10 is 20."
"So?", said the adult.
"So if 10 + 10 is 20, and if 9 is one less than 10, then 9 + 9 is 19."
By asking the child to explain her thinking, the adult learned a great deal. For one thing, the child was not guessing. And the 19 did not result from faulty memory. The five year old’s thinking was very complex. The child had subtracted one 1 rather than two. She had made a cosmetic error, not a structural error.
"Ah, I get it, " said the adult. "So tell me. What’s 9 + 10?"
"That’s 19," said the child. "Wait a minute. That other thing you gave me, 9 + 9? That’s 18!"
The notion that children act thoughtfully and that their thought is worth knowing about is an essential aspect of a teacher's approach to children’s learning.
For one thing, the origin and the development of children’s ideas is a fabulously rich field of study in itself. It is called genetic epistemology and it was invented by the Swiss philosopher, Jean Piaget, who with colleagues world-wide conducted sixty years of seminal research on children’s ideas and their development.
For another, it is simply very practical. To know about a child’s thinking makes a teacher’s job much easier. Children are not mere adults, the same as we are but less experienced. Nor are they empty vessels waiting to be filled up by the teacher (or the parent). To know about children’s thinking puts the teacher in a position to nutrify the child’s thinking; to help it to become more robust, more efficient, more coherent, more generalizable. To know about children’s thinking is essential.
The Present Research
This work had its beginning in a math methods course taught in the Clayton, Missouri public schools during the spring semester of 1996.
The problem at hand arose from the January 23, 1996 issue of The New York Times where two problems were reported as having been used with young children in Japan.
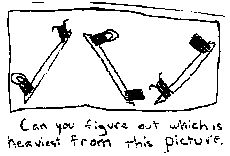
Take a look at the drawing on top. In each case tell which animal is the heaviest.


Problem T (Three Animals) Problem F (Four Animals)
Each week, as a major part of the class, participants were given "childwatching" tasks to perform so that they could get to know children’s thinking in a wide variety of mathematical situations. One week they agreed to try these problems with their schoolchildren and to report on their findings at our next weekly meeting.
The purpose of the activity was to find out about children’s thinking, not to assess a particular child in order to give him a grade. Here you see the teacher as researcher—as genetic epistemologist in the sense of looking in on the genesis and development of children’s knowledge.
The results give a glimpse into the development of thought on two simple problems from the first beginning steps that children take to some very complex extensions of the original problems constructed by pupils in the upper grades of elementary school.
Make some guesses as to how children solved the problems. What would five year olds do? How about eight year olds? If you said, "a night and day difference," you are right.
Results were reported at each age from 3 through fifth grade.
Three Year Olds
Many three year old students appeared to be very confused when asked to tell which one was the heaviest. When shown the seesaw pictures, they would answer by pointing to the picture instead of calling the object by name. When asked why they thought the "bear" or "racoon" was heaviest, they would usually have no response or they would simply say "I don’t know" or "It just is." If questioned further about their choice, they would sometimes change their minds and choose another animal.
Four and Five Year Olds
In contrast to the three year olds, four and five year olds responded with confidence and were not confused by the question but focused on superficial physical characteristics as can be seen in the ensuing dialogue. Here are the results:
Problem T:
Child 1: "The racoon is the heaviest because he has bigger eyes and he’s down." "If he had smaller eyes, would he still be heavier?" "No."
Child 2: "The boy is heavier because he is bigger." "Of all of them, the bear is the heaviest because he’s the biggest."
Child 3: "The racoon is the heaviest because of his tail. It’s on the seesaw and the bear’s is not."
Child 4: "The bear is the heaviest. He has a tail and the boy doesn’t."
Child 5: "The heaviest of all is the bear because he’s big."
Child 6: "The racoon is the heaviest because of his tail. It’s on the seesaw and the bear’s is not."
Child 7: "The bear is the heaviest. He has a tail and the boy doesn’t."
Child 8: "The heaviest of all of them is the racoon because he is never up." This is an extraordinary response at such an early age. It amounts to an algorithm: "If an animal is never up, it’s the heaviest.
Problem F:
Child 9: "The rabbit is heavier because he has bigger ears."
Child 10: "The panda. . .because he’s cute."
Child 11: "The squirrel because of his tail."
Child 12: "The boy is the heaviest. Even though the rabbit has a tail, the rabbit is smaller than the boy.
Child 13: "The panda is heaviest because the rabbit is smaller."
Child 14: "The boy is heaviest because he’s a boy."
Child 15: "Of all of them (in the 4 friends group), "The bear is the heaviest because he’s the biggest."
First Grade
Almost all of the responses we received indicated that prior knowledge of the animals in real life determined the solution to this problem. We expected that our older students and/or more capable math students would be able to conserve mass and could apply higher level reasoning to this problem. However, almost all of our students, regardless of age or ability, based their responses on the physical attributes of real animals or their interpretations of the level of the seesaw/animals in the picture.
Examples of incorrect responses on Problem T include:
Child 1: "The boy is heaviest because the one that's up is the heaviest."
Child 2: "The boy because in real life people are heavier."
Child 3: "The clown because if it's doing tricks the things would make it heavier."
Child 4: "The bear because racoons are littler. You can tell the weight by the size."
Child 5: "The bear is the heaviest because the seesaw seat is lower."
Child 6: "The bear because the bear is big, he eats people, and he's the strongest."
A handful of students were able to demonstrate higher level reasoning and arrive at the correct response. Examples of these responses on Problem T include:
Child 9: "The racoon because it's heavier than the bear."
Child 10: "The racoon because he's heavier than the bear and the bear's heavier than the boy."
Child 11: While pointing to the two animals at the lower ends of the seesaws, she said, "So the bear and the racoon are the heaviest. Then looking at these two together on the left seesaw added, "Oh, so the racoon is the heaviest."
Second Grade
Physical characteristics of real-life animals and idiosyncratic attention to detail continued to characterize second graders’ answers. But transitivity (a is bigger than b, b is bigger than c, so a is bigger than c) plays a role as well.
Problem F:
Child 1: After looking at the pictures for a while, the child touched the picture in several spots and finally ran his finger across the bottom of the balances very slowly. He then answered, "The squirrel, because it’s the furthest down." I think he meant it was the furthest down on the paper.
Child 2: The child first asked me what the second animal was. He looked at the picture for a few seconds and then replied, "The fox or the person." I asked him why he chose those two. He said, "A person can lift a racoon and a rabbit. A fox can also lift a racoon, but a person can lift a fox."
Child 3: The child looked at the picture for only a few seconds and then replied, "Probably the squirrel. Because there’s only one of him and he’s on the bottom. (pause for a few seconds) And besides this is heavier than this (pointing to the person and the rabbit), this is heavier than this (pointing to the rabbit and the panda), and the squirrel is heavier than this (pointing to the squirrel and the person.)
Third and Fourth Grade
Idiosyncratic attention to detail ("His tail goes below the bench seat of the see-saw" and "His see-saw is the lowest") continues to play a role in some children’s explanations. Real life attributes ("Bears are heavier than rabbits" seemed to diminish (but we didn’t interview every child). Mature solutions become more common.. Here an example of a fourth grader’s systematic procedure:
Child 2, a strong student academically, closely examined the pictures of the animals. Without discussion he replied, "the dog [squirrel], because the rabbit is heavier than the panda and the boy is heavier than the rabbit and the dog [squirrel] is heavier than the boy".
And this method is algorithmic—efficient and almost mechanical:
Child 3, an average student, responded, "The fox isn’t showed anymore, OK, it’s the fox." She went on to explain her reasoning. "The rabbit is up, then down. That means it’s not the heaviest. The person is up and down again, so it isn’t the heavier. The panda is always up. It’s the lightest. The fox is always down." She initially predicted that the fox was the heaviest, because it was only pictured once and on the bottom. Then she reasoned by considering each pair of animals to determine if her answer was correct.
Many fourth graders responded in a manner to those given above.
Grades Three through Five (from a resource teacher)
In the children’s answers I observed conclusions based on previous extraneous knowledge, for example "Bears are heavier than squirrels." Another was on partial information, ignoring information given in one of the three drawings. Some students were overwhelmed by the question, giving a response because it was expected of them, but not providing logical reasoning.
The next group of students had the ability to keep multiple things in mind. This is necessary for the type of comparisons and reasoning necessary for the seesaw problem. This group used comparisons that included all members, "It’s the cat (racoon) because he is heavier than the bear and the bear is heavier than the person." Some used comparisons that included all members based on systematic comparison "1 is heavier than 4, 4 is heavier than 3. Therefore 1 is heavier than 4 and 3, but 2 is heavier than 1 so 2 is heavier than 1,3,4."
Some made comparisons that included all members based on logical inference, "2 is heavier than 3, and 3 is heavier than 1, therefore 2 is heavier than 3 and 1."
One student used systematic, exhaustive elimination of all components and made comparisons by a process of elimination. "The rabbit could not be the heaviest because on one picture he is up and on the other he is down. The person couldn’t for the same reason. And the Panda couldn’t either because he is going up on the one picture. So it must be the squirrel."
A fourth grade boy worked by process of elimination, crossing out animals based on comparisons. "In the first drawing, we eliminate the rabbit. In the second drawing, we eliminate the panda and in the third, we eliminate the person."
By visual comparison and elimination a fourth grade girl discovered, "I figured it out by simply looking to see which animal was never on top. I checked it with the method I used on the other side (comparison by process of elimination)".
Finally, one student made a comparison using a middle ground or point of comparison "To get the answer, you have to compare the two pictures by using the bear."
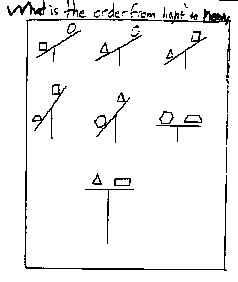
Other students who had responses to the problem were very enthusiastic about the development of their own seesaw problems. They added other elements to the problem, increasing the number of components, added unnecessary or incorrect information, providing variations in the degree of the angles of the seesaw, and extending the depth of the requested response.

Summary and Discussion, Thomas C. O'Brien
Teachers can do more than assess whether children's answers to trivial textbook exercises such as 9 + 9 = ___ are correct. And even if they are used to probing the underpinnings—the fabric—for children's answers to curricular questions, they can go further. They can learn about cognitive fabrics which underlie children's thinking and which are more basic than this or that topic in a school curriculum. In this case the issue was logical necessity, an issue of fundamental importance in thinking.
In the present childwatching, teachers from pre-school to grade 5 conducted interviews of children on two simple but provocative problems:
1. All the teachers, as a matter of routine professional practice, were used to going beyond textbook answer-scoring in order to find out why a child answered as she did in a particular curricular activity, problem or exercise. That is, in the 9 + 9 story in the Introduction, they too would have thoughtfully asked the child, "How come?" rather than merely judging the response right or wrong. But to look in on cognitive issues not connected with the curriculum was new and fascinating and fruitful, and in many cases the results were surprising.
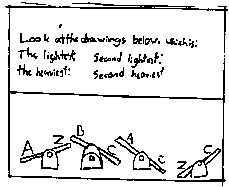
2. In the short age span observed, teachers observed the growth of children's thinking from a) apparently not understanding the question, to b) Piagetian magic (implying a causal relation between two phenomena when they are only accidentally related ("It's the racoon because of the big eyes," "It's the squirrel because his swing is the lowest."), to c) Piagetian realism ("The boy is heaviest because in real life people are heavier."), to d) transitivity ("The racoon because he's heavier than the bear and the bear's heavier than the boy."), to e) the construction of an algorithm ("If an animal is down and never up, it's the heaviest."), to f) understanding logical necessity and going beyond it to the creation of problems in which there is no logically necessary answer and problems involving inconsistent information.
3. The answers within a class ranged very widely. Indeed, Kaplan (pre-school) reports that at least one of her pre-school children developed an algorithm involving logical necessity: In Problem 1 "It's the racoon because he's never up."
Gwyn, the resource teacher, reports in follow-up conversation that among Grade 4 children, there were answers based on magic and on realism and on parsimonious home-made algorithms ("Never up"), as well as the creation of original problems involving logical ambiguity and inconsistency.
4. Some of the teachers tried to assess the relation between children's school achievement and performance on the present task. It is true that many high achievers were able solvers of the "Bear" problems, but this was not always so, and some low achievers were able solvers of the "Bear" problem. This is an issue for further study.
What is the significance of the present work, other than the fact that teachers did some childwatching which they found engaging?
It seems to me that the teachers' research has some important implications:
It is clear that children's thinking is very different from the thinking of adults. In American education curriculum makers commonly agree that the cup of knowledge that a child has is less full than that of an adult and we commonly view the teacher's role as "filler of the child's cup of knowledge." There is another aspect of the issue and it gets very little attention. Much more important is the fact that what's in the child's cup of knowledge is intrinsically different from that of most adults. Virtually no adult invokes big eyes as evidence that this animal is heavier than that. And virtually no adult applies Piagetian realism—bears are big and ferocious in real life—as evidence in judging the weights of the animals in the present problems.
It seems obvious that children's thinking is different from adults' and it is often the case that children's thinking is less mature than that of adults. This fact should have enormous effects on the work of curriculum makers and teachers, who often think that the job of education is to fill children to an adult level. In particular, the pervasive role of magic and realism in the present reports should be considered by curriculum makers and teachers whose concerns are logical necessity and cause and effect, and transitivity.
It seems from the present research that children may commonly work in advance of most adults in terms of intellectual risk-taking and adventurousness, witness the fourth graders' original "Bear" problems. This fact should have enormous effects on the work of curriculum makers and teachers. What about the role of children as problem devisors? Look at the complexity of problems created by the fifth graders.
A major aspect of Piagetian research is the organism's tendency toward equilibrium. But it is an equally major aspect of a Piagetian view of cognition that humans do not merely tend toward equilibrium. They actively search for and construct disequilibrium - new mountains to conquer. In the present research we see children's active construction of equilibrium. And in the original problems provided by the resource teacher we see the construction of disequilibrium par excellence.
Susie Bargiel
Kathy Feely
David Hoffman
Lee Scissors
Sharon Steinberg
Jan Wilson
Captain Elementary School
6345 Northwood
Clayton, MO 63105, USA
Linda Gwyn
Glenridge Elementary School
7447 Wellington Way
Clayton, MO 63105, USA
Carolyn Myers
Susan Wise
Meramec Elementary School
400 South Meramec
Clayton, MO 63105, USA
Carol Kaplan
Family Center
301 North Gay
Clayton, MO 63105, USA
Davi Turman
East Alton Public Schools #13
10 St. Louis Ave.
East Alton, IL 62024, USA
Thomas C. O’Brien
School of Education
Southern Illinois University
Edwardsville IL 62026, USA
Tom O'Brien <74055.652@compuserve.com>