Howard Walter
An investigation into the affective profiles
of girls from single-sex and co-educational schools,
as they relate to the learning of mathematics.
Submitted by Howard Maurice Walter to the University of Exeter for the degree of Master of Education in Mathematics Education, 1997.
Summary.
Central to this dissertation is an attempt to investigate whether or not a single-sex environment has a positive impact upon girls' attitudes and beliefs, as they pertain to the learning of mathematics. It is argued that all learners of mathematics are enveloped by the social practices pertaining to both mathematics and society at large. Underlying these social practices are a multiplicity of environmental and learner-related variables that may result in a differential and discriminatory experience for girls. It is proposed that each of these variables has to be identified, understood, and acted upon in an attempt to combat these discriminatory forces. This paper focuses on one major component of the learner-related domain — that of affect. Based upon existing research and theoretical analyses, this study attempts to identify important affective variables and the role that they play in the learning of mathematics. An investigation into these affective components, as they pertain to girls educated in a single-sex and a co-educational environment in Bermuda, has been carried out. Data were collected through the use of a questionnaire and subjected to quantitative analyses. The dissertation finds that, for the sample used, the co-educational environment may lead to a degree of affective impairment for girls, particularly with regard to confidence. Additionally, it is suggested that the more positive affective profiles of the single-sex educated girls should become the reference point for further analysis, thus annulling the view that girls are somehow deficient. It also proposes that the classroom situation cannot be seen in isolation; instead, investigations pertaining to mathematics and gender should account for gender-specific norms and values that are reinforced and promoted by elements contained within the wider socio-political domain.
Table of Contents.
| Introduction. | |
| Chapter 1: Gender-Related Attainment Differences in Mathematics. | |
| Chapter 2: Review of Research into Gender-Related
Differences in Mathematics Attainment. |
|
| Chapter 3: An Increase in Research Focus on the
Affective Domain. |
|
| Chapter 4: Components of the Affective Domain. | |
| Chapter 5: The Single-Sex Environment. | |
| Chapter 6: The Investigation. | |
| Chapter 7: Results. | |
| Chapter 8: Discussion of the Findings. | |
| Chapter 9: Conclusions and Recommendations. | |
| Appendix 1: Student Questionnaire. | |
| Appendix 2: Fennema-Sherman Mathematics Attitude Scales. | |
| Appendix 3: Results. | |
| References. |
List of Tables and Figures.
| Table 1:
1995 grade distributions for Year 5 BSSC examinations, by gender. |
|
| Table 2:
Environmental and learner-related variables considered important in the analysis of gender differences in the learning of mathematics. |
|
| Table 3:
Stability and locus of causality dimensions for Weiner's attributions. |
|
| Table 4:
The effects of attributional properties as they relate to positive and negative outcomes. |
|
| Table 5: The properties of Weiner's four attributions. | |
| Table 6:
Summary of the research into the attributional styles of girls and boys. |
|
| Table 7:
Split-half reliabilities, as calculated by Fennema and Sherman for their attitude scales. |
|
| Table 8:
Attributional impact upon student affective profiles for success and failure outcomes. |
|
| Table 9: Combined scores for success and failure attributions. | |
| Table 10:
Significance levels for the differences between means for the single-sex educated girls' groups versus the co- educated girls' groups. |
|
| Table 11:
Significance levels for the differences between means for the single-sex educated girls' groups versus the co- educated boys' groups. |
| Page: | |
| Table 12:
Significance levels for the differences between means for the co-educated educated girls' groups versus their male peers. |
72 |
| Table 13:
Distribution of the success and failure attributions for each group of students.
|
73 |
| Figure 1:
Graph illustrating the percentage of girls and boys obtaining A-C grades or equivalent in mathematics at GCSE/GCE/CSE. |
17 |
| Figure 2:
The reproductive cycle of gender inequality in mathematics education. |
24 |
| Figure 3:
A cyclical model of the conclusions of the research of John Ernest. |
25 |
| Figure 4:
Box and whisker plot of the total affective profile scores for each group of students. |
64 |
| Figure 5:
Series of graphs showing the distribution of the mean scores obtained by each group of students on individual affective components. |
65-70 |
| Figure 6:
Graph showing the distribution of the mean scores obtained by each group of students across all affective components. |
76 |
A brief overview of the key elements of the study of gender and the learning of mathematics is given in this introduction. From this, an indication of the rationale for focusing on the affective domain is developed. The aims and significance of this investigation are also outlined. All of these elements are expanded upon in later chapters. The main hypothesis statement and definitions of key terms, utilized throughout the text, are also included.
Burton (1986) informs us that girls' poor participation and achievement rates in mathematics became an issue, particularly in the United States of America, during the 1960s. Since that time, a considerable amount of research has been carried out in an attempt to understand and, thereby, alleviate the obstacles encountered by women and girls in this area. For some time, replicable differences, of moderate magnitude, favouring boys in tests of mathematical attainment have been discerned (Maccoby and Jacklin, 1974; Benbow and Stanley, 1980; Dossey et. al., 1988; Maccoby, 1990; Wilt et. al., 1991).
Such a situation has serious implications for females and, consequently, for society as a whole, because of the importance that is placed upon success within this field of study. Mathematics, as Sells (1973) points out, can be seen as a 'critical filter', whereby the pursuits of an individual, in the realms of vocational, leisure and academic activities, can be constricted by a lack of mathematical knowledge; thus, this apparent 'female' impairment is clearly an issue of considerable concern.
As we shall see, a great deal of research has been undertaken in an attempt to find explanations for gender differences in the learning of mathematics. Increasingly, this research has emphasized the role that social processes play, a position illustrated by Ernest (1994), who suggests that "girls' differential experiences . . . constructs them as gendered learners." (page 56).
This claim is based on the view that the learner of mathematics is enveloped by the social practices pertaining, not only to mathematics, but also to society at large. Consideration will be given to those environmental variables that may underlie these social practices; for example, the school, the peer group, wider society, the teachers, and parents.
It will be claimed that no single environmental variable alone will determine a student's success or failure, but, instead, that these variables operate in a complex network. Consideration will also be given to the reciprocal interaction between the individual and the components that comprise the environment in which he or she is enveloped.
Internal to these individuals are what can be described as learner-related variables. These include those within the cognitive and the affective domains. When these learner-related variables are considered in conjunction with the environmental variables, a network of inter-relationships can be envisaged that takes on considerable complexity.
Each environmental and learner-related variable that may help mediate differential experiences for girls has to be identified, understood, and, where appropriate, acted upon by those responsible for the provision of mathematics education.
Central to this dissertation is one major component of the learner-related domain — that of affect. Based upon existing research and theoretical analyses, important affective elements are identified and the role they play in the learning of mathematics is discussed. These elements include confidence, the usefulness of mathematics, mathematics as a male domain, attitude toward success, and attributional style. The term ‘student affective profile’ is utilized to describe the students' beliefs and attitudes as they relate to these components. Further consideration is given to existing theory and research in an attempt to determine those attitudes and beliefs, pertaining to these affective components, that may contribute positively to student success in the learning of mathematics. Students displaying a tendency towards these attitudes and beliefs are described as having a more ‘positive affective profile’.
An investigation is carried out centered upon the following hypothesis:
‘With regard to the study of mathematics, girls educated in a single-sex environment display a more positive affective profile than their female contemporaries from a co-educational background.’
The findings reported in the research literature are compared with those obtained in this investigation. Consideration is also given to possible wider implications of the affective profiles displayed by the students in this study.
It should be noted that the significance of this investigation can be seen from two perspectives. From a broad, i.e. international, perspective, the very fact that girls and women are being discriminated against justifies all efforts at investigation in itself; however, there are also components that are significant locally. Whether or not the single-sex environment available in Bermuda contributes positively to the girls' affective profiles, when compared with the co-educational alternatives, is important. Additionally, as the head of the mathematics department at the only remaining all-girls school in Bermuda, it is important that I am able to discern, not only what constitutes a positive affective profile, but also to what degree the girls within the school are aspiring to that profile. Based upon this information, steps can be taken towards affective enhancement where necessary.
Chapter 1: Gender-Related Attainment Differences
in Mathematics.
The taste for the abstract sciences in general and, above all, for the mysteries of numbers is very rare: this is not surprising, since the charms of this sublime science in all their beauty reveal themselves only to those who have the courage to fathom them. But when a woman, [who] because of her sex, our customs and prejudices, encounters infinitely more obstacles than men in familiarizing herself with their knotty problems, yet overcome these fetters and penetrates that which is most hidden, she doubtless has the most notable courage, extraordinary talent and superior genius.
Gauss (quoted in Leder, 1992, page 597)
In the light of the fact that Gauss made this observation in 1807, it is quite clear that the suggestion of a gender-related problem in the learning of mathematics is not a new one. In this chapter, the nature and extent of this problem will be considered from the perspective of gender-related differences on tests of mathematical attainment. Research and theoretical analyses from several countries will be discussed and consideration will be given to the situation as it pertains to Bermudian high school students.
From their research with high school students in the United States, Maccoby and Jacklin (1974) concluded that some replicable differences exist, of moderate magnitude, favouring boys in tests of mathematical achievement. Since that time, Maccoby (1990) informs us, the research into gender differences has become more sophisticated, particularly in the use of meta-analyses that reveal, not only the direction of gender differences, but also quantitative estimates of their magnitude. She goes on to contend that much of this more recent research continues to confirm the direction of gender differences in favour of boys. There is evidence to suggest, however, that this is becoming increasingly less pronounced; for example, the American Association of University Women (1992) notes that "meta-analyses comparing recent research with studies done in 1974 indicate a significant decline in gender differences." (page 24). Such a view is supported by the research findings of Baker and Jones (1993), in which they compared data on mathematical achievement from the 1964 First International Mathematics Study (FIMS) with those of the 1982 Second International Mathematics Study (SIMS). From their analysis of eighth-grade students in nine countries, they found that in 1964 only Israeli females surpassed their male counterparts on measures of mathematical performance. By 1982, these gender differences had declined in all but one of the nine countries, and females from Belgium, Finland, Sweden, and the United States were now surpassing their male contemporaries. Other researchers who report declines in gender differences in mathematical performance include Friedman (1989) and Penfold (1991).
There is evidence to suggest that the prevalence of gender differences in tests of mathematical achievement increases with the age of the students. Dossey et. al. (1988), for example, give details of the 1986 research carried out by the National Assessment of Educational Progress at Educational Testing Service. In their survey of 34,000 North American students, they found that gender differences in mathematics performance at the primary level was not significant, but a slight difference in favour of boys was detected for students of age 17. Similarly, from her wider analysis of research carried out in the United States, Australia, and Britain, Leder (1990a) concludes that there are few consistent gender-related differences in performance in mathematics at the primary school level. She goes on to indicate, however, that there is "a substantial body of evidence to suggest that, from the beginning of secondary schooling, males frequently outperform females in mathematics." (page 13). This view is also supported by Shuard (1986), who conducted research on behalf of the Cockcroft Committee into differences in mathematical performance between girls and boys in the United Kingdom.
The research of Baker and Jones (1993), referred to earlier, also tends to support the contention that gender differences are less prevalent among younger students, particularly when viewed in conjunction with the work of Hanna, Kundiger and Larouche (1990), who also analyzed the 1982 SIMS data. Their focus was on grade 12 students from fifteen countries, in which responses to questions pertaining to seven areas of mathematical study were analyzed. Where gender-related differences were found for these older students, they were consistently in favour of boys. It was only in one country, Thailand, that no significant difference was found on all seven mathematical areas. Interestingly, the results from Belgium and Finland suggest a considerably higher level of performance by their grade 12 boys, which appears to be in contrast with the findings for their grade 8 students, reported by Baker and Jones (1993).
It is apparent from the works of Baker and Jones (1993) and Hanna, Kundiger and Larouche (1990) that the degree of difference between male and female students varies considerably across countries and across different areas of mathematical study. Leder (1995), from her meta-analysis of cross-cultural data, confirms the generality of the findings that "some performance differences, typically in favour of males, continue to be reported." (page 213). It is clear that such a generalization, as Isaacson (1989) points out, is and continues to be a cause for concern internationally.
No formal analysis of gender differences in student performance in mathematics has been carried out in Bermuda; however, the Department of Education has made the 1995 Bermuda Secondary School Certificate (BSSC) examination results available for this investigation. The BSSC is taken by all students in the Government schools. The examination can be taken at one of three levels: the Traditional level, which is regarded as 'academic' and is based upon the University of London GCE, syllabus B; the less academically rigourous Commercial level, which focuses on business mathematics, although some geometry and algebra have recently been introduced; and the General syllabus, which is designed for those who experience difficulty with the subject. Table 1 details the 1995 grade distributions for the three levels of the Year 5 BSSC, by gender.
Table 1: 1995 grade distributions for Year 5 BSSC examinations, by gender.
Traditional Mathematics |
||||||
Percentage of Exam Group |
Percentage of Year group |
|||||
Grade |
Boys |
Girls |
Boys |
Girls |
||
A |
24.3 |
18.1 |
8.1 |
7.4 |
||
B |
21.4 |
13.8 |
7.1 |
5.6 |
||
C |
50.0 |
50.0 |
16.7 |
20.3 |
||
D |
1.4 |
11.7 |
0.5 |
4.8 |
||
E |
2.8 |
6.4 |
1.0 |
2.6 |
||
Total Percentage of Year Group |
33.4 |
40.7 |
||||
Commercial Mathematics |
||||||
A |
9.1 |
9.4 |
4.3 |
4.8 |
||
B |
8.1 |
9.4 |
3.8 |
4.8 |
||
C |
37.4 |
34.2 |
17.6 |
17.3 |
||
D |
15.2 |
21.4 |
7.1 |
10.8 |
||
E |
30.3 |
25.6 |
14.3 |
13.0 |
||
Total Percentage of Year Group |
47.1 |
50.7 |
||||
General Mathematics |
|||||||
A |
0.0 |
0.0 |
0.0 |
0.0 |
|||
B |
0.0 |
0.0 |
0.0 |
0.0 |
|||
C |
36.6 |
0.0 |
7.1 |
0.0 |
|||
D |
36.6 |
35.0 |
7.1 |
3.0 |
|||
E |
26.8 |
65.0 |
5.2 |
5.6 |
|||
Total Percentage of Year Group |
19.4 |
8.6 |
|||||
Before analyzing these results, it is important to consider their limitations. This data is the single largest measure of attainment in mathematics for students in Bermuda. The results pertain to 441 students in their final year of high-school, 210 boys and 231 girls. This represents approximately 75% of all students in this age group, the remaining 25% attending schools outside the government system. The fact that students from independent schools do not take this examination and are, therefore, not included in this data, suggests that it may be subject to 'selectivity bias', whereby non-school factors, such as socioeconomic background, affect choices made by families in regard to the school that they select for their children. Thus, the degree to which these results pertain to island-wide attainment patterns in mathematics for this age group, is open to question. Although these results are the most recent available, it would be unwise to suggest that any achievement patterns discerned are representative of what may be expected in other years; hence, the following analysis should be treated with caution.
From the results, it can be seen that 40.7% of the girls took the Traditional level examination compared with only 33.4% of the boys. The majority of candidates for this examination come from the two 'academic' schools, where students are selected by means of an examination in English and mathematics at age 11. For many years, the number of girls gaining places in these schools has surpassed that of the boys. This may, therefore, explain why more girls than boys take the Traditional level and fewer take the General level examination. It should be noted that the level of examination selected for each student is determined by past examination performance and teacher recommendation.
Despite the fact that more girls in this sample took the Traditional examination, they did not obtain as many A and B grades as their male contemporaries — 13% of girls and 15.2% of boys. This pattern of results may have a negative impact with regard to girls' opportunities for higher education in Bermuda because it is these grades that are considered by the Bermuda College as pre-requisites for admission to their associate degree programme.
The distribution of the grades for the middle level Commercial examination are fairly similar for both genders, although 1.5% more of the girls in the year group obtained grades in the A/B range for this examination. Once again, however, the representation of the girls in this examination was higher than that of the boys — 50.7% versus 47.1%.
For the General level examination, neither gender was awarded grades in the A/B range, and, in the case of the girls, only D's and E's were obtained; however, only 8.6% of the girls took this examination compared with 19.4% of the boys.
In summary, if the results are considered across all three BSSC levels, then, for this sample, there do appear to be gender-related differences in mathematics attainment, in that the distribution of the results for the girls is more leptokurtic in nature than that of the boys. Thus, more girls are tending to achieve grades in the middle of the distribution, whereas boys are represented more highly at the very highest and at the very lowest levels of attainment. The larger proportion of boys represented at the highest grade levels is particularly noteworthy, as this situation appears to replicate findings in the wider international context. Leder (1990a), for example, reports that studies carried out in the United States, the United Kingdom, and Australia indicate that a significantly higher number of boys obtain the top grades in tests of mathematical performance.
The Bermudian students who comprise the subjects of this investigation will take three widely used external examinations. In their fourth year of high school, they take the North American Preliminary Scholastic Assessment Test (PSAT), followed by the Scholastic Assessment Test (SAT) in year 5. Also in year 5, they will take the United Kingdom based General Certificate of Education (GCSE). It is appropriate, therefore, to consider the research carried out with regard to gender-related performance on these examinations.
Despite the apparent convergence in achievement for boys and girls, Sadker and Sadker (1994) report that, for the PSAT and the SAT, the most important and widely administered North American tests, the gender gap remains disturbingly apparent. They detail the 1991-92 results, in which the number of males obtaining scores in the top categories for PSAT was 18,000, outstripping their female contemporaries by over 10,000. This is despite an attempt by the developer of the test, Educational Testing Service (ETS), to reduce this gender gap by giving twice the weight to verbal performance scores, an area that it perceives as a traditional 'female' strength.
The PSAT is an important element of the North American education system because the results are used to select winners of the prestigious National Merit Scholarships (for which two out of three semi-finalists are male), and many states and colleges use them as a basis for awarding their own scholarships. In addition, as Sadker and Sadker (1994) point out, "the PSAT serves as an early indicator of the winners and losers in the great SAT contest soon to follow." (page 138).
Despite being a major critic of the SAT, Owen (1991) acknowledges the important role that it plays in the education system of the United States, pointing out that "virtually all the nation's most selective colleges — and a great many less selective ones — require their applicants to submit SAT scores." (page vii). Furthermore, several employers require recent college graduates to submit these scores when applying for jobs, despite the illegality of this practice.
Serious implications arise from these requirements as they pertain to girls, because on a scale of 200 to 800, males typically outscore females by several points on the mathematics section. This is illustrated by the most recent results, detailed by the College Entrance Examination Board and Educational Testing Service (1996). For the mathematics section of the test, the 1995 results show average scores of 490 and 525 for girls and boys respectively, with each group rising by 2 points in 1996 to 492 and 527 respectively; thus, the boys maintained average scores that were 35 points higher than their female contemporaries.
The College Entrance Examination Board and Educational Testing Service (1990) maintain that their tests are a common measure of student performance. Furthermore, they contend that lower female scores are not a function of the test but a function of the different educational experiences that boys and girls receive, and are, therefore, indicative of a real educational problem (cited in Sadker and Sadker 1994, page 155). There are several critics who question this claim of objectivity; for example Owen (1985), Bridgeman and Wendler (1990), McCornack and McLeod (1988), Wainer and Steinberg (1990), and Horner and Sammons (1989). In addition, they suggest that the contribution that these tests make to a discriminatory environment cannot be ignored.
It is clear then that the lower scores being achieved by girls may lead to reduced educational and vocational opportunities.
In the United Kingdom, where the GCSE examination is based, trends similar to those in the United States have been identified with regard to gender differences in mathematics performance. The facts that boys perform on average better than girls and that fewer girls than boys engage in mathematics at school and beyond have been well documented; for example, Cockcroft (1982), the Royal Society and the Institute of Mathematics and its Applications (1986), the Open University (1986), and Mills et. al. (1993).
Additionally, the Assessment of Performance Unit (1988) found that the superiority of boys develops during secondary schooling and "that there is no difference in performance between the sexes at age 11, or even that girls are ahead of boys at that age." (page 22). They also indicate that "where differences are found, the clearest differences between boys and girls are amongst high attainers (the top 10-20 percent)." (page 23). The Department of Education and Science (1988) also notes significant improvements in the mathematical attainment of girls and this appears to continue to be the case, as is illustrated by the GCSE/GCE/CSE results represented in the graph below.
Figure 1: Graph illustrating the percentage of girls and boys obtaining A-C grades or equivalent in mathematics at GCSE/GCE/CSE.
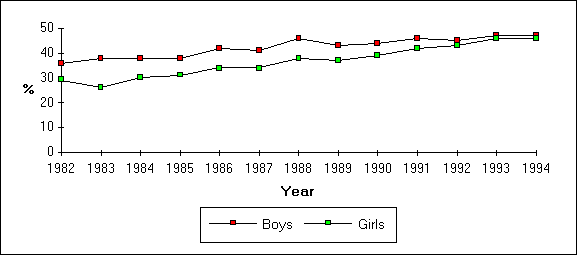
Sorce: Department of Education and Science (1982-94), Annual Reports of Statistics of Education Public Examinations CSE/GCE/GCSE.
These results tend to indicate that the problem of lower female attainment, as measured by these examinations, is diminishing but is not necessarily eradicated. While a gender difference exists, it will continue to be problematic, in that it has wider implications for women in society — as we shall see.
In the next chapter, consideration will be given to the research into possible explanations of gender-related differences in mathematics performance.
Chapter 2: Review of Research into Gender-Related Differences in Mathematics Attainment.
In this chapter, it will be argued that there has been a shift away from biological explanations of gender differences in mathematics achievement towards explanations that incorporate both environmental and learner-related variables. This movement will be discussed in terms of changes in the philosophical foundations of the research. From this philosophical analysis, the role that affect might play in the generation of gender-related differences in mathematics achievement is theorized. It is proposed that this theoretical position lends justification to the investigation of the affective domain in an attempt to address the problems encountered by females in their study of mathematics.
A Biological Perspective.
An extensive body of literature was developed during the 1960s and 1970s that proposed possible biological factors as being responsible for gender differences in the learning of mathematics. Sharman points out that some of these theories have centred on a "recessive gene on the X-chromosome, the role of sex hormones, and differences in brain lateralisation." (quoted in Ernest 1994a, page 28). In addition, some research has focused on differences in spatial visualization; for example, Eddowes suggests that boys display a superiority in spatial and mechanical tasks in the primary years and that this gives them a firmer foundation for mathematics and science at the secondary school level (cited in Burton 1986, page 23).
These biological explanations contrast with the findings of several researchers who reject this view on the grounds of oversimplification and lack of evidence; for example, Fennema and Sherman (1977), Burton (1986), Tatre (1990), and Leder (1992). Shuard (1982) de-emphasizes the issue of spatial visualization on two counts: firstly, that its link with mathematical ability is not fully understood; and, secondly, by referring to the 1967 findings of Husen, which suggest that gender differences in mathematical attainment vary across different countries, thereby suggesting that other factors may impact upon attainment. This latter view is supported by the more recent research of Baker and Jones (1993) and Hanna, Kundiger and Larouche (1990), details of which were discussed earlier.
Mahony (1985) brings an interesting critical perspective to the biological argument and states:
In order to create social division between two groups some actual difference is needed as a legitimating explanatory category. Biology and difference in biology, far from explaining differences in behaviour between boys and girls, is used to give legitimacy to them. Gender differences do not flow naturally from biology but must be seen as rooted in politics. The appeal to biology is merely an excuse and as such must itself be seen as part of the rationalizing of the politics of male domination.
Mahony (1985, page 64).
Benbow and Stanley (1980) co-authored a paper in which they expressed a preference for a genetic explanation of the differences in mathematical precocity. This, as Tobias (1993) points out, revitalized the notion of the existence of a 'male math gene', a notion that was taken up and widely promoted by the American popular press. An interesting response was elicited, however, from Egelman et. al. (1981), in which they state:
An underlying fallacy . . . is the notion that, if a trait is under genetic control, the expression of that trait is immutable . . . One has only to consider something as simple as the height of wheat to realize that a particular genetic strain of wheat will yield different ranges of height in different environments. A determination of the height in one environment will tell one nothing about the height in a substantially different environment.
Egelman et. al. (1981, page 116).
This view leads to the contention that other factors should be investigated when considering the differential levels of achievement in the learning of mathematics, as related to gender.
A Broader Perspective: Environmental and Learner-Related Variables.
A multiplicity of environmental and learner-related factors has been posited in the various models and explanations contained within the literature on gender differences in the learning of mathematics. Upon examining a selection of these models, Leder (1992) concludes:
The various models described share a number of common features: the emphasis on the social environment, the influence of other significant people in that environment, students' reactions to the cultural and more immediate context in which learning takes place, the cultural and personal values placed on that learning and the inclusion of learner-related affective, as well as cognitive variables.
Leder (1992, page 609).
Table 2 summarizes the component factors inherent within the environmental and learner-related variables that Leder (1992) discerns as being of importance in attempts to analyze differences in the learning of mathematics.
Table 2: Environmental and learner-related variables considered important in the analysis of gender differences in the learning of mathematics.
Environmental Variables |
Learner-Related Variables |
| Cognitive Variables: | |
School |
Intelligence |
Teachers |
Spatial Abilities |
Peer Group |
Affective Variables: |
Wider Society |
Confidence |
Parents |
Fear of Success |
Attributions |
|
Persistence |
It is acknowledged by many researchers, Leder (1992) and Shuard (1982), for example, that these component factors do not function in isolation. As Leder (1992) states: "an implicit thread running through the review [of the research] is the link between the different components selected and the reciprocal interaction between factors in the environment and the individuals who function in it." (page 610).
A Philosophical Shift.
In reviewing the various theoretical models and explanations that have been proposed to account for the observed gender-related differences in mathematical attainment, Dunne and Johnston (1994) summize that three dominant stands can be identified, each determined by its underlying philosophical foundations. They relate these strands to the work of Habermas, who identified three knowledge constitutive interests: technical, practical and emancipatory. In turn, Grundy applies these terms to the educational domain by suggesting that "these interests constitute three types of science by which knowledge is generated and organized in our society. These three ways of knowing are empirical-analytic, historical-hermeneutic and critical." (quoted in Dunne and Johnson 1994, page 223).
When categorizing research, a degree of flexibility is required; for example, Dunne and Johnston (1994) take a valid critical position "which centres on the absence of an explicit recognition of the politics of knowledge constitution in the technical and practical positions." (page 223). It should be recognized, however, that the practices and techniques adopted by researchers working from these positions can also generate valuable knowledge that can only be enhanced when subjected to the rigours of analysis from a critical perspective.
A valuable component of categorization is that it facilitates the identification of philosophical shifts in the foundations of the research. The movement away from biological investigations towards more social explanations for gender differences in mathematics attainment is characterized by an accompanying philosophical shift. Dunne and Johnston (1994) describe this in Habermas' terms as from those determined by technical interests to those representative of practical interests. They also note a parallel shift in terms of the research methodologies that tend to be adopted, from those of a quantitative nature to a more qualitative approach.
The importance of this shift lies in the recognition of the environmental context as a contributory mediator of gender differences; thus, in broad terms, there is a drift away from focusing upon what the learners are bringing to their environments, via their innate abilities, to focusing upon the influence that these environments have upon the development of the learners contained within them. As Ernest (1991) points out, the implication of such a perspective for the learners is that they are far more comparable at birth than after years of socialization; "thus 'abilities' are conferred on students by their experiences." (page 208).
Dunne and Johnston (1994) go on to argue that the 'critical' position espoused by Habermas provides a more powerful platform for the development of research in this field than those of the technical and practical positions. They contend that:
Through a critical analysis, the social and political contexts which circumscribe the production of knowledge are made explicit and are recognized for the constitutive role they play in the production and validation of knowledge. This is the case for both the arena which is being researched and for what counts as research.
Dunne and Johnston (1994, page 224).
Lather extends Habermas' framework in her discussion of research methodologies by suggesting a fourth position related to post-structuralism (cited in Dunne and Johnston 1994, page 223). Walkerdine and the Girls and Mathematics Unit (1989) illustrate this position by applying the post-structuralist theory of Foucault and others in their analysis of gender differences in mathematics. They espouse the view that "no real human subject exists prior to the social practices within which she is subjected." (page 206). Furthermore, they go on to suggest, these social practices derive from an overpowering ideology that encompasses sexism in both society and mathematics, and the myth of male superiority in mathematics. By the same argument, it can be assumed that, as constituents of the learners' social practices, the environmental and learner-related variables identified earlier are enveloped by this overpowering ideology, therefore contributing to gender differences in the learning of mathematics.
The Reproductive Cycle of Gender Inequality.
McCormick (1994) suggests that gender stereotypes are views held about males or females that are based on assumptions which are often exaggerated and inaccurate (either favourable or unfavourable). They are prejudiced thoughts or beliefs that may have very little correspondence with reality, yet they are used to describe all members of a sex. She goes on to argue that commonly accepted sex stereotypes can drive and perpetuate a cycle of sexism. She contends that:
The assumptions underlying the stereotypes manifest themselves in different expectations for treatment of boys and girls in the classroom and this negatively affects their ability to achieve their full potential.
McCormick (1994, page 45).
All of the environmental variables outlined in Table 2 — the schools, the teachers, the peer group, the parents, and wider society — are potential agents of sexism within this cycle. The individuals who comprise these component groups can either reinforce or undermine the cycle of sexism. Unless teachers, for example, challenge the assumptions underlying gender stereotypes, their students, as adults, may continue to model traditional functions at home and in the workplace. Thus, the perpetuation of these traditions might, in turn, reinforce the prejudicial assumptions that are held about the appropriate roles for men and women, thereby maintaining a cycle of sexism.
Gender stereotyping also plays a role in the cycle of sexism proposed by Ernest (1991), in which he encompasses both the socio-political realm and the educational realm as it pertains to mathematics education. This is illustrated in Figure 2 below.
Figure 2: The reproductive cycle of gender inequality in mathematics education.
Educational Realm Socio-Political Realm
Lack of equal opportunities Gender stereotyping
in learning maths
Girls' perceptions of mathematics Reproduction of gender
and own abilities in mathematics inequality in society
Girls' lower examination attainments Women getting
and participation in mathematics lower paid jobs
Source: Ernest (1991, page 276).
John Ernest, an early pioneer in the field of gender and mathematics, also explained the conclusions of his research by way a cyclical model. These conclusions, as detailed by Tobias (1993), suggest that:
Society expects males to be better than females at mathematics. This affects attitudes; attitudes affect performance; performance affects willingness to study more mathematics; and, eventually, males do better than females.
Tobias (1993, page 74).
Figure 3 illustrates these findings.
Figure 3: A cyclical model of the conclusions of the research of John Ernest.
Societal Expectations:
Boys are better than girls at mathematics
Boys outperform girls Undermines girls' attitudes
in mathematics to mathematics
Undermines girls' persistence Undermines girls' performance
in mathematics in mathematics
The two cyclical models pertaining to mathematics explicitly incorporate affective components. Figure 2 includes girls' perceptions of mathematics and their own abilities in mathematics, and Figure 3 proposes a link between societal expectations and girls' attitudes towards mathematics. Both models, therefore, suggest that affect can play a contributory role in the perpetuation of the cycle of gender inequality in mathematics. It would seem, then, that the investigation of the affective domain may be justified as one possible route through which attempts can be made to address these problems of inequality.
Addressing the Cycle of Gender Inequality in Mathematics.
All people . . . in a school system have a responsibility for stopping the cycle of sex-stereotyping and sexism. Since sexism has been ingrained in us for centuries, breaking this barrier and changing the system so that it is equitable will not be swift or easy. Such change in schools requires group effort by all educators, not just women. Sexism is a human problem, not a woman's issue.
McCormick (1994, page 47).
As can be seen from Figure 2, the cycle of inequality encompasses components from the broader socio-political realm as well as from the educational realm. This, then, places the problem of gender-related differences in the learning of mathematics within society as a whole, not just within the educational domain. However, as Ernest (1991) points out, if we are to address the problem of inequality, "any would-be solutions must be multiple, attacking each stage of the transmission in the cycle . . . " (page 275).
Parker et. al. (1995) suggest that the teachers of mathematics have a key role to play in the translation of gender-equity policy into gender-equitable practices. These teachers are in a position to influence several of the components of the cycle of gender inequality, thereby enabling them to help free their students from this cycle. In turn, this freedom may help provide the opportunity for these students to develop more fully their academic, personal, and occupational potentials, and to explore a variety of options that may previously have been closed to them.
The motivation behind the development of this investigation is to understand the affective components that relate to girls' perceptions of their own mathematical abilities; thus providing an informed basis from which an attack upon this component of the cycle of gender inequality can be launched.
Chapter 3: An Increase in Research Focus on the Affective Domain.
In this chapter, it will be argued that a philosophical shift pertaining to beliefs about the nature of mathematics and developments in psychological learning theory have resulted in a growing consensus amongst researchers that affective components may play a part in producing gender-related differences in mathematics achievement.
An Increasing Recognition of the Importance of Affect.
The students are a major part of [a school's mathematical] environment. The attitudes and beliefs that students hold about the subject and about themselves as learners of mathematics contribute as much to that environment as do the concrete and cognitive aspects of mathematics. It is not likely that students will be highly motivated to persist in the study of mathematics if little attention is given to the development of their attitudes and beliefs about mathematics (their mathematical affect). A mathematical environment cannot be considered to be healthy if any one of its individual components is not functioning to its full potential.
Blum-Anderson (1989, page 3).
The role that the affective component plays in gender-related differences in mathematics achievement has increasingly become the focus of research. This is illustrated by the recent work of Ma and Kishor (1997), who carried out a meta-analysis to integrate and summarize the findings of no less than 113 primary studies in this field. (Their findings will be referred to in a later section).
Seegers and Boekaerts (1993) suggest that the increased focus of research on the affective domain is due to a growing consensus among researchers that differences in mathematical attainment cannot be explained as solely the result of differences at the cognitive level. They further espouse the view that "an adequate explanation has to account for complex interactions among cognitive, affective and motivational variables." (page 133).
A Philosophical Shift.
It may be that a philosophical shift pertaining to beliefs about mathematics as a subject underlies this growing consensus. In recent years, several feminist theorists, Damarin (1995) and Campbell (1995), for example, have charged that mathematics is male-centred in both its content and processes; that is, that the discipline is a product of masculine thinking. Noddings (1996) points out that these theorists contend that the highly abstract nature of traditional mathematical thought is a masculine artifact and, thereby denies the social nature of mathematics. By separating mathematics from its social settings and cultural origins, a constrained view of the discipline has been created that incorporates infallibility, noncontingency, austerity, and absolutism. Thus, as Ernest (1994a) suggests, mathematics is widely perceived as "difficult, cold, abstract, theoretical, ultra-rational, but important and largely masculine." (page 5), perceptions that he describes as relating to the absolutist philosophies of mathematics.
Such an image, Brown (1984) argues, results in a curriculum which is "de-peopled in that contexts and concepts are for the most part presented ahistorically and unproblematically." (page 12). Willis (1989) suggests that this projection of the culture of mathematics contrasts with 'female' culture in fundamental ways and tends to inhibit girls' involvement in the subject. This, in turn, conspires to limit attainment and thus acts as a critical filter, denying access in both academic and vocational pursuits.
Ernest (1994a) argues that it is a vital task of the educational and scientific community to shift this largely androcentric image of mathematics to one that incorporates a more humanized view, a position that he equates with the fallibilist philosophies of mathematics. Fallibilism views mathematics as a complex interaction of a multiplicity of components that make up the social process. As Ernest (1994a) says, "this view embraces as legitimate philosophical concerns the practices of mathematicians, its history and applications, the place of mathematics in human culture, including issues of values and education — in short — it fully admits the human face and basis of mathematics." (page 8). Such a philosophical shift allows for the culture of mathematics to be influenced by 'female' perspectives which, Brown (1984) argues, might emphasize context, boundedness, differences between situations and problems, and 'people-connectedness'.
There is evidence which suggests that when mathematics programmes are built upon such perspectives, they are of benefit to girls. Isaacson (1989), for example, gives details of the introduction of an alternative mathematics curriculum introduced in Holland, which incorporated a higher 'social' content making use of broader-based applications that were more obviously and immediately relevant to students. She goes on to report that this resulted in a higher proportion of girls studying mathematics to the age of 18.
Similarly, Morrow and Morrow (1995) detail the successes that have been achieved through the "SummerMath" programme which has been held for a number of years at the campus of the Mount Holyoke College in the United States. This programme is designed to address the ways in which women are underserved in mathematically based fields, by providing mathematical experiences in which the learners are encouraged to build upon and incorporate their experiences as females. Through this programme, Morrow and Morrow (1995) have found that their students leave "feeling more able to persist in doing mathematics problems, more aware of the usefulness of mathematics, and dramatically more confident." (page 21).
In addition, Willis (1989) contends that the traditional, absolutist view of mathematics "is not essentially male but reflects a particular construction of masculinity also inappropriate for a great many boys." (page 32). Thus, the pedagogy and content of much of school mathematics may be responsible for the exclusion of many children, irrespective of gender. School mathematics curricula will always represent a selection from a much wider body of knowledge; however, a more humanized curricula, that does not restrict 'female' perspectives, may result in greater student access.
Developments in Psychological Learning Theory.
Developments in psychological learning theory may also have contributed to an increased focus upon the affective domain. Daniels and Anghileri (1995) argue that the twentieth century has seen a transition from the perception of the learner as someone who only receives knowledge to one who is actively involved in constructing knowledge within a culturally situated community, a shift from a behaviourist to a constructivist perspective. Thus, as McLeod (1992) contends, the perception of the role that the learner plays in the learning process must lead to different research approaches in both the cognitive and affective domains. He further states that "the behaviourists have generally been reluctant to look closely at the underlying processes that are related to affective responses." (page 577). However, as Snow and Farr have reported, the perception of the learner as central to the knowledge construction process has resulted in the emergence of affect as an important part of cognitive theory (cited in McLeod 1992, page 577).
Chapter 4: Components of the Affective Domain.
In this chapter, an analysis of the research literature is carried out in an attempt to identify the components of the affective domain that are considered to impact upon gender differences in the learning of mathematics.
McLeod (1992) suggests that the affective domain can be divided into the component elements of beliefs, attitudes, and emotions. He further states that these elements describe a wide range of affective responses to mathematics and that they can be distinguished in terms of their stability and level of intensity. In general, beliefs and attitudes tend to be more stable, while emotions may be subject to rapid change. McLeod (1992) suggests that the level of intensity of the affects that they describe increase from "cold" beliefs about mathematics to "cool" attitudes related to liking or disliking mathematics to "hot" emotional reactions to the frustrations of solving nonroutine problems." (page 578).
This investigation will focus upon student belief systems and their attitudes pertaining to the study of mathematics.
Beliefs and Gender Differences.
In the realm of mathematics education, McLeod (1992) identifies four sub-domains to which student beliefs pertain. These include beliefs about mathematics, mathematics teaching, self, and the social context. From their review of the considerable amount of research that has been carried out in these sub-domains, Meyer and Koehler (1990) have identified five components that impact upon gender differences and the learning of mathematics. These include confidence, the perception of the usefulness of mathematics, beliefs pertaining to the perception of mathematics as a male domain, the fear of success, and attributional style. An examination of these components and the ways in which they interact may help in understanding the contribution that they might make to gender differences in mathematics achievement.
(i) Confidence in the learning of mathematics.
Many researchers have stressed the relationship between student confidence in their own mathematical ability and their achievement in the subject. Pedersen et. al. (1985), for example, examined the relationship between nine different affective variables and achievement in mathematics amongst 1,937 seventh- and eighth-grade students from thirteen junior high schools in the United States. They found confidence to correlate higher with achievement than with any other affective variable (r = 0.43). A similarly high level of correlation (r = 0.41) was found by Fennema and Sherman (1977) in their study of nearly 3,000 high school students. From his meta-analysis of research carried out in this area, Kloosterman (1988) concludes that self-confidence "has a stronger correlation with achievement than do other affective variables." (page 345).
Confidence relates to how sure a student is of his or her ability to do well on a mathematical task or to learn new mathematics; thus, the link between confidence and persistence within the subject is important. As Fennema states: "One tends to do those things that one feels confident to do and to avoid activities that arouse anxiety." (quoted in the Open University 1986, page 43). Walkerdine and the Girls and Mathematics Unit (1989) also contend that "pupils' reading of their own mathematical ability may be influential in determining their future pursuit of the subject." (pages 182-3). Such a view is supported by several other researchers — for example, Armstrong and Price (1982), Eccles (1983), Lantz and Smith (1981), and Sherman (1982).
The studies carried out by Pederson et. al. (1985) and Fennema and Sherman (1977), referred to earlier, also considered the relationship between self-confidence and gender. Pedersen et. al. (1985) found that seventh-grade females scored significantly higher than their male contemporaries on levels of confidence in learning mathematics; however, this was no longer the case by the eighth grade, as females' scores had decreased, while those for the males had increased.
Fennema and Sherman (1977) found that when a gender difference in mathematics achievement was discerned in favour of males, it was accompanied by gender differences in confidence, also in favour of males. Furthermore, Badger (1981), also reporting on the Fennema-Sherman findings, suggests that:
The fact that girls were significantly less self-confident in their mathematical ability before they showed any signs of poorer performance tends to confirm the influence of this variable on performance.
Badger (1981, page 232).
(ii) The usefulness of mathematics.
Pedersen et. al. (1985) found a correlation between student perception of the usefulness of mathematics and achievement in the subject (r = 0.35). They also reported that seventh-grade females scored higher on this variable than did their male contemporaries; however, they also found that, as students became older, the scores declined for females and increased for males.
Armstrong and Price (1982) found that the perceived usefulness of mathematics ranked as the number one reason among students for continuing to pursue the subject. Meyer and Koehler (1990) argue that this perception may be a major influence upon participation on a short term basis, even when the difficulty of the material increases. They suggest that motivation to persevere with a particular task is a product of the student's expectancy of success and his or her perception of the value of the task. Thus, even if the student's confidence, and therefore expectancy of success, is low, but a strong perception of the usefulness of the task is held, motivation to continue may result, irrespective of the difficulty.
Using their scale, designed to measure students' beliefs about the usefulness of mathematics currently, and in relationship to their future education, vocation, or other activities, Fennema and Sherman (1976a, 1977) found that high school males in general scored higher on this variable. In addition, Eccles (1983) found that males felt that mathematics was of more value to them than did females, and Lantz and Smith (1981) concluded that the attitudinal variable most highly correlated with mathematics participation was the subjective value placed on the subject.
(iii) Mathematics as a male domain.
Koehler and Fennema (1982) claim that individuals tend to do those things that they perceive as appropriate for their gender. Such a view might impact upon the value of mathematics. As discussed earlier, the widely held perception of mathematics as being androcentric in nature may serve to fulfil itself and thereby present a barrier to females. If, as Isaacson (1989) suggests, a girl believes that engagement in mathematics is inappropriate for females, then her success in the subject may conflict with her perception of appropriate sex-role fulfillment. On the other hand, as Meyer and Koehler (1990) contend, "sex-role congruency is not likely to be as important for males, since the prevailing stereotype is that mathematics is a masculine domain and therefore a very appropriate subject for male study and achievement." (page 64). Furthermore, as Koehler and Fennema (1982) point out, individuals may "fear sanctions from others if they perform opposite sex-stereotyped activities. In relation to mathematics, females may fear social rejection if they excel in mathematics, while males will be pressured into doing well." (page 102).
In spite of the theoretical significance of this variable, Meyer and Koehler (1990) report that the research in this area has yielded mixed results and it has not been useful in predicting either participation or achievement in mathematics. However, they go on to contend that it is the interaction of this variable with others that may make it more or less important, hypothesizing, for example, that this belief may become more or less potent as a function of age and maturity. Additionally, Fennema indicates that stereotyping occurs at a crucial time and suggests that it is probably "more than just coincidence that at adolescence, when girls are becoming increasingly aware of their sex role, sex-related differences in mathematics learning appear." (quoted in Koehler and Fennema 1982, page 102).
(iv) The fear of success.
Leder (1992) and Meyer and Koehler (1990) reiterate the link between the fear of success and sex-role congruency described above. They cite the work of Horner, in which she describes the fear of success as the fear of the negative consequences that accompany success. She further identifies two sources of these negative consequences: firstly, the individual's possible loss of her sense of femininity and self-esteem; and, secondly, social rejection as a result of the success.
Leder (1992) integrates confidence with sex-role congruency and the fear of success. She suggests that the notion of the fear of success is consistent with the lower confidence expressed by females in relation to their mathematical ability, their greater tentativeness with regard to the appropriateness of participating in mathematics and that this may, ulitimately, result in their lower performance in the subject. She goes on to conclude that:
Work carried out within the fear of success paradigm suggests that females' lower performance in mathematics is a function of internalization of, and conforming to, the expectations of others, rather than being a function of ability per se.
Leder (1992, page 615).
(v) Attributional Style.
Prominent in the literature on gender differences in mathematics is the way in which a student attributes causation for success and failure. Central to much of this work is Weiner's Attribution Theory. Bell-Gredler (1986) informs us that Weiner identified ability, effort, task difficulty and luck as the most likely causes attributed to various academic outcomes. To each of these causes he attributed the dimensions of stability and locus of causality. Stability of the perceived cause refers to the endurance of the particular attribution. Since ability and objective task difficulty are enduring, they are seen as stable. In contrast, effort and luck are transient and therefore unstable. Locus of causality refers to the origin of the perceived reason for the outcome; i.e. the environment (external) versus the individual (internal). In this way, ability and effort are internal to the individual, while luck and task difficulty are external.
A summary of the elements of Weiner's theory of attribution, provided by Fennema (1981), is shown in Table 3.
Table 3: Stability and locus of causality dimensions for Weiner's attributions.
LOCUS OF CAUSALITY
Internal |
External |
|
| Stable | Ability |
Task Difficulty |
| Unstable | Effort |
Luck |
Source: Fennema (1981, page 99)
Bell-Gredler (1986) indicates that two functions are fulfilled by the causal dimensions. One is that they contribute to the goal expectancies of the individual; for example, stability contributes to unchanged expectations for the future — i.e. failure which is attributed to a stable cause is expected to be repeated. The second function relates to the emotional reactions generated by each attributional dimension. These reactions, in turn, contribute to belief systems and are, therefore, influential upon future behaviour. Internal attributions for success have the potential for enhancing the self-esteem of the individual, while failure attributed internally can contribute to a negative self-image. In contrast, no impairment of self-esteem is expected if failure is attributed to external factors.
Table 4 summarizes the effects of attributional properties in relation to positive and negative outcomes.
Table 4: The effects of attributional properties as they relate to positive and
negative outcomes.
| Positive Outcomes: | |
| Stable | Continued expectations for success |
| Emotions of pride maximized | |
| Unstable | Does not decrease success expectation |
| Emotions unlikely to be extended to future situations | |
| Internal | Contributes to positive sense of self-worth |
| Enhances the likelihood of engagement in future tasks | |
| External | Unrelated to self-image |
| Negative Outcomes: | |
| Stable | Continued expectations for failure |
| Emotions of shame, apathy, resignation maximized | |
| Unstable | No decrease in success expectancy |
| Emotions likely to be extended to future events | |
| Internal | Contributes to negative self-image |
| Enhances the likelihood of avoidance of achievement tasks | |
| External | Unrelated to self-image |
Source: Adapted from Bell-Gredler (1986, page 286).
Table 5 summarizes the properties of the four major attributions.
Table 5: The properties of Weiner's four attributions.
| Attribution | Dimension | Consequences |
| Ability | Internal | Generates feelings of competence or incompetence |
| and feelings of pride or shame | ||
| Stable | Same outcome expected again; emotions of pride | |
| and shame magnified; for failure, resignation and | ||
| apathy magnified | ||
| Effort | Internal | Generates feelings of pride for success |
| Unstable | Does not decrease success expectancy | |
| Luck | External | Self-image not altered |
| Unstable | No decrease in success expectancy | |
| Task | External | No enhancement of self-esteem for success outcome |
| difficulty | Stable | Same outcome expected again |
Source: Adapted from Bell-Gredler (1986, page 287).
Some interesting research findings have resulted from the application of attribution theory to gender differences in the learning of mathematics. Leder (1992) and Taylor (1990) detail the research conducted by Wolleat, Pedro, Becker and Fennema, in which they studied the attribution patterns pertaining to the learning of mathematics of 647 female and 577 male high school students. Their findings indicate that females, more strongly than males, attributed success and failure in mathematics according to a pattern described as 'learned helplessness'. Kloosterman (1988) informs us that students characterized as learned-helpless feel that success is beyond their control and that effort is unproductive because it probably will not lead to success. Thus, Dweck found, such students tend to demonstrate a low level of persistence and avoid challenges where possible (cited in McLeod 1992, page 585). Kloosterman (1988) summarizes the research findings on attributional styles of these students by stating that they "often attribute failures to the stable, uncontrollable factor of a lack of ability and attribute their successes to the external, uncontrollable factors of an easy task or good luck." (page 346). He cites the conclusion of many researchers that such students see little hope for academic success. Leder (1992) further informs us that Wolleat et. al. found that the attributional patterns of high attaining females were particularly dysfunctional. "Sex differences in attribution to effort in response to success events are most pronounced at the highest level of achievement." (quoted in Leder 1992, page 601).
From her meta-analysis of the research, Reyse reports that there is "a well established relationship between attributions and achievement-related behaviours such as persistence, effort, and choice of challenging tasks." (quoted in Taylor 1990, page 56). Furthermore, she confirms gender differences in patterns of attribution for success and failure in that females are "more likely to see success as caused by effort and less likely to see success as caused by ability." (quoted in Taylor 1990, page 56).
Several commentators have detailed these findings — for example, Burton and Townsend (1985), Cockcroft (1982), Russo (1984), and Badger (1981). Table 6 summarizes the generalized conclusions of this research.
Table 6: Summary of the research into the attributional styles of girls and boys.
SUCCESS AT MATHS |
LACK OF SUCCESS |
|
| BOYS | Skill, Ability |
Bad luck, Lack of effort |
| GIRLS | Good luck, Effort |
Lack of skill & Ability |
Source: Ernest (1994b, page 44).
By combining the generalized results above with the attributional properties outlined earlier in Table 5, the implications for boys' and girls' learning in mathematics can be discerned. Feelings of competence and pride might result from boys attributing their success to skill and ability. For girls who attribute their success to having made a good effort, feelings of pride might also be generated and their expectancy for success may not be decreased; however, if luck is attributed to their success, then, due to its external nature, self-image may not necessarily be enhanced.
Conversely, by attributing their lack of success to luck, boys may not experience the diminution of their self-image. If lack of effort is attributed, then the expectancy of future success does not necessarily decrease. For girls who attribute their lack of success to a lack of skill and ability, feelings of incompetence and shame may be generated, and resignation and apathy might also be magnified.
As Seegers and Boekaerts (1996) state: "a self-derogating bias in attributional style will quasi-automatically lead to lower motivation and performance." (pages 219-20). Badger (1981) supports this view and states that:
The obvious corollary to such findings is that girls will lack persistence on tasks where there is no rational basis for continuing to expend effort. On such tasks, luck can hardly be relied upon for continued success and a lack of ability is not conducive to continued effort.
Badger (1981, page 235).
She further suggests that the importance of this interpretation of girls' attributional patterns is not as a direct explanation of their apparent lower performance than boys, but as an explanation of why they do not persist in their mathematical education.
Certainly there appears to be evidence to suggest that girls and women are underrepresented in higher level mathematics courses, although this situation does appear to be improving. In the United Kingdom, the engagement of fewer girls than boys in mathematics at A' level has been documented by Cockcroft (1982) and Burton (1986). Friedman (1995) gives details of the number of women obtaining degrees in mathematics in the United States: at the bachelor level this has increased from 23% in 1950 to 47% in 1992; for the same time span, the figures have increased from 20% to 39% at the masters level and 6% to 21 % at the doctoral level.
As Morrow and Morrow (1995) point out, the under-representation of women at these higher levels of mathematics education has a serious impact upon their career opportunities. From their analysis of the career statistics published by the National Research Council, they found a large disparity between the genders in participation rates in quantitatively based fields; the more a particular career requires mathematics, the higher the pay, and the lower the rate of female participation.
It is clear that attribution patterns, along with confidence, mathematics as a male domain, the perceived utility of mathematics, and attitude toward success are all important affective components that merit investigation as they pertain to gender-related differences in mathematics achievement. These components, therefore, will form a central part of this dissertation.
Chapter 5: The Single-Sex Environment.
Research into single-sex schooling and achievement will be considered in the first part of this chapter. This will be followed by an analysis of research that has considered the various affective components, discussed in the last chapter, as they pertain to girls in single-sex schools.
Achievement and Single-Sex Schooling.
Until recently, single-sex education was perceived as an anachronism, reflective of outdated beliefs that the educational needs of males and females are different. Co-education was assumed to be the path through which similarity of treatment of the two genders could be achieved, a view reflected in the 1972 North American law, designed to abolish sex-discrimination in the public schools, Title IX of the Education Amendments, in which single-sex provision was made illegal.
In the United Kingdom, the voluminous researches of Dale (1969, 1971, 1974) set the agenda for thinking in this field for many years. He concluded that the attainment levels reached by co-educated pupils is, in general, higher than those for pupils educated in single-sex environments. More recently, research carried out by Smith (1986) suggests that single-sex groupings for mathematics failed to improve the performance of girls. However, Shaw (1995) contends that "a growing number of professional educationalists have returned to thinking well of single-sex education. This is quite a U-turn and largely the result of the introduction of league tables which consistently show how well single-sex schools do, particularly day schools for girls." (page 129).
Interpretation of the league tables requires caution as they tend to be comprised of raw data drawn from public examination results. When viewed from this perspective, Smithers and Robinson (1995) acknowledge the impressive results obtained by many single-sex schools; however, they suggest that "they are not of themselves evidence that single-sex education is the more effective, even specifically in relation to academic achievement." (page 1). Instead, they suggest that the apparently superior performance of girls' schools could, among other things, be due to the following:
(1) ability intake
(2) social class background of the pupils
(3) type of school involved
(4) history and tradition of the schools, and
(5) better performance by girls overall.
Hugill and Narayan (1995) report, however, that an analysis of the league tables carried out for Ofsted, the United Kingdom Government quango responsible for school inspections, still indicates better performances from students educated in single-sex schools after adjustments for the various factors outlined above have been made.
In the domain of achievement in mathematics and science, Smithers and Robinson (1995) suggest that, when ability is controlled for, the apparent positive effects of single-sex schooling for girls is nullified; however, it should be noted that their conclusions are drawn from data obtained on 14-year olds in the International Study of Educational Achievement carried out some twenty-five years earlier. Whilst acknowledging that their work is illustrative of some of the many flaws associated with the league tables of school results, it may be that the data upon which their conclusions are based need to be re-evaluated to account for the social-historical context from which they were drawn. They may not reflect, for example, the effects of attitude changes about sex-roles within the last decade; thus, a wider and more up to date review of research into the mathematics education of girls may have resulted in conclusions of a different nature.
Over recent years, numerous studies from around the world suggest that there are achievement advantages, particularly for females, in single-sex schools. Eales (1986), for example, details an experiment, carried out in a secondary school in the United Kingdom, in which the effectiveness of single-sex groupings was tested in an attempt to arrest the decline of female performance in mathematics. After two years, it was found that the attainment levels of the girls had improved, as measured by their 'O' level and CSE results; furthermore, a significantly greater number of girls were opting for 'A' level mathematics.
In Jamaica, Hamilton (1985) considered the GCE examination results of 1,146 students. Samples were drawn from 3 single-sex boys' schools, 5 single-sex girls' schools, and 7 co-educational schools. From her results, she presents "the relative standing of each group based on overall performance — first placed girls from single-sex schools, then boys of this type, followed by boys from co-educational institutions, and finally, their female counterparts." (page 543). Similarly, Hiddleston (1995) found from her research in Malawi that females who attended girls-only high schools achieved better results on the final school examination than those who attended co-educational institutions. She also notes that school selection is independent of the academic standing of the students; thus, there is no apparent bias towards placing the best girls in single-sex schools. Similar findings are also reported by Lee and Lockheed (1990) from their research in Nigeria.
At the post secondary school level, Delon (1995) details the merger of an all-male school with an all-female school from the 'Ecoles Normales Supereure' system in France. She reports that, in the eight years since this amalgamation, the number of female students opting to study mathematics has declined by 80%, a situation which leads her to conclude that "in no subject were the consequences as disastrous as in the area of mathematics." (page 142).
As has been discussed, there are problems associated with the interpretation and analysis of league tables of school examination results. Similar problems may also pertain to the contemporary research into the effectiveness of single-sex versus co-educational schools. It is suggested by Smithers and Robinson (1995) that various school and non-school factors should be taken into account. The role of school characteristics has been addressed extensively in much of the recent research but, increasingly, the importance of non-school characteristics pertaining to the personal and family background of the students has also been recognized.
In their research, for example, Lee and Bryk (1986) and Riordon (1985) have made attempts at controlling such factors as social class, race, number of parents, religion, and family income as they pertain to the entry level characteristics of students attending single-sex versus co-educational schools. Jimenez and Lockheed (1989) extend this further by considering 'selectivity bias', whereby non-school factors such as socioeconomic background, innate ability, and individual motivation affect choices made by families with regard to the type of school they select for their children. From their investigation, they conclude that "failure to correct for selection biases results in a significant underestimate of the positive effect of single-sex schools in enhancing female achievement." (page 135).
All three studies outlined above are consistent with regard to the conclusion that "single-sex schooling is more effective for female students." (Jimenez and Lockheed 1989, page 117). Findings such as these lead Burton (1990) to summize that:
Surely a change in social groupings does not affect women's abilities although there is ample evidence that it does affect their achievement.
Burton (1990, page 2).
The findings of Ma and Kishor (1997) may give us some insight into why the single-sex environment might lead to enhanced achievement levels. Conducting a meta-analysis of 113 primary studies concerning the relationship between attitude toward mathematics (ATM) and achievement in mathematics (AIM), their findings suggest that gender does not have a significant effect on the relationship between ATM and AIM. However, they did find:
Studies with mixed-gender groups tended to show a weaker
ATM-AIM relationship than studies with separate gender groups, indicating that pooling male and female students together might have a weakening effect on the relationship.
Ma and Kishor (1997, page 37).
Such a conclusion suggests that the affective dispositions of students toward mathematics needs to be considered with reference to their educational environments, single-sex or co-educational. The next section outlines some of the research that has been carried out in this regard.
Affective Components and Single-Sex Schooling.
Throughout the research literature concerning girls in single-sex schools, there are numerous references to the affective components discussed earlier. As we shall see, much of this research concludes that these girls are displaying more positive affective profiles; however, such a conclusion is not universal. In the United Kingdom, Smith (1986) describes an experiment carried out to investigate the effectiveness of single-sex mathematics sets on the performance levels of students and their affective dispositions towards the subject. He found that the establishment of such sets failed to improve the self-confidence of more able girls and that segregated girls regard mathematics as a less useful subject than their peers from either co-educational or all male sets. The results also suggest that "girls apparently regard maths as a more difficult subject than boys whether they have been taught maths in single-sex sets or not." (pages 21-22).
These findings are in contrast with those detailed by Marjoram (1994) and Gwizdala and Steinback (1990) who concluded from their studies that girls in single-sex groups gained more in self-confidence and achievement than those in co-educational groups.
It has been suggested by several researchers that the co-educational classroom experience for girls can act as an agent of the wider social expectations of them, and that these impact negatively upon their levels of confidence. As Orenstein (1994) found, "by sixth grade, it is clear that both girls and boys have learned to equate maleness with opportunity and femininity with constraint." (page xiv).
Sadker and Sadker (1994) investigated the behaviour of girls in co-educational and single-sex classrooms. Their findings are represented by the words of one teacher who stated: " "When it's all female, the girls take chances. But when guys are in the class, the girls stop asking questions the way they do now. They begin to say things like, 'I'm not sure if this is the right answer
but . . .' " " (page 236). Similar perceptions of this type of classroom situation were also reported amongst the students themselves, many of the girls citing fear of ridicule and intimidation by boys as reasons for their withdrawal.
Walden and Walkerdine (1986) argue that constraint associated with femininity allows for the following of the procedural rules of mathematics and the behavioural rules of the classroom which are necessary for task completion in many cases. They go on to suggest, however, that 'real understanding' requires the internal rules of mathematical discourse to be challenged and that "such challenging requires considerable confidence because it necessitates the recognition that rules are to be simultaneously followed and challenged. . . . many girls do not have such confidence, nor would dare to make a challenge." (page 145). Thus, they conclude that such a situation locates girls at "the nexus of a constellation of practices characterized by tortuous and contradictory relationships between gender . . . and intellectuality." (page 144).
The importance of the role of confidence is exemplified by this analysis. Additionally, it may give some explanation to the conclusion of Kloosterman (1988) that self-confidence "has a stronger correlation with achievement than do other affective variables." (page 345).
Winchel, Fenner and Shaver (1974) found that for girls "who attend co-ed elementary schools, fear of success is more common, and it appears to be increased by attendance at co-ed high school." (page 729). They attribute these findings to the cross-sex competition found in co-educational classrooms. More recently, Jimenez and Lockheed (1989), reviewing large scale studies carried out in New Zealand and Canada, report that girls in single-sex schools had a greater desire to be remembered as brilliant students in comparison with girls in co-educational schools.
Lee and Lockheed (1990) concluded from their study with Nigerian students that single-sex schools affect girls positively through the engendering of less stereotypical views of mathematics as a male domain.
A multifaceted study involving 1,807 secondary students carried out in the United States by Lee and Bryk (1986) found:
Whether concerning academic achievement, achievement gains, educational aspirations, locus of control, sex-role stereotyping, or attitudes and behaviors related to academics, results indicate that single-sex schools deliver specific advantages to their students, especially female students.
Lee and Bryk (1986, page 381).
Two studies undertaken by Foon (1988) in Australia and Cairns (1990) in Northern Ireland replicate the results obtained by Lee and Bryk (1986) as they pertain to academic self-esteem and locus of control. Both conclude that being a student at a single-sex school may contribute to an increased sense of cognitive competence and a more inner-orientated locus of control.
Other researchers who have concluded that single-sex environments contribute positively to girls' affective dispositions include Eales (1986), Burton and Townsend (1985), the Open University (1986), and the National Coalition of Girls Schools (1993). A review of a broad spectrum of research in this field leads Sadker and Sadker (1994) to conclude that:
. . . the evidence is persuasive. Girls in single-sex schools have higher self-esteem, are more interested in non-traditional subjects such as science and math, and are less likely to stereotype jobs and careers.
Sadker and Sadker (1994, page 233).
However, perhaps the more cautionary position taken by Valerie Lee should be noted. She is an influential and well respected University of Michigan researcher who has conducted numerous studies pertaining to single-sex education in the United States and internationally. (Examples include, Lee and Bryk, 1986; Lee and Lockheed, 1990; Lee and Marks, 1990 and Lee, Marks and Byrd, 1993). When interviewed by Sadker and Sadker (1994), she was asked if she had reached a decision about the merits of single-sex education. Her response was that the evidence led her to take an equivocal position and she emphasized that:
So much depends on the school. Some girls' schools we saw looked like throwbacks, nineteenth-century finishing schools to prepare little ladies. But other girls' schools really are paying attention to gender — what is in the books and on the walls, as
well as the interaction. They encourage assertiveness, curiosity, and questions.
(quoted in Sadker and Sadker 1994, page 249).
Such a cautionary note may be particularly pertinent when consideration is given to the investigation that will be described in the next section. As will be seen, this will focus upon the affective profiles of students drawn from the only remaining single-sex girls' school in Bermuda; thus, any conclusions drawn can not be viewed as widely generalizable.
Chapter 6: The Investigation.
Rationale and Methodology.
Ernest (1994), citing the work of Habermas, suggests that the motive which underlies the quest for knowledge defines the interest behind the educational research paradigm. The primary aim of this investigation is to collect data pertaining to the affective profiles of girls educated in a single-sex and a co-educational environment. The motivation behind this aim is that the data obtained may provide an informed basis from which the affective component of the cycle of gender inequality can be addressed. Such an approach aligns this investigation with the critical theoretic research paradigm, because, as Ernest (1994) points out, the interests of this paradigm include the achievement of social justice which is sought through the outcome of improved social institutions and conditions.
The rationale for this investigation is derived from the previous research that has been outlined earlier. This rationale stems from a position of critical analysis that proposes that girls' differential experiences in the realm of mathematics education are a result of an environment that comprises a reproductive cycle of inequality derived from an overpowering ideology that encompasses sexism in both society and mathematics. However, in an attempt to understand and attack the affective component of this cycle, quantitative approaches that are more usually associated with the scientific paradigm will be utilized.
Such an approach derives from an epistemological position which acknowledges the role of theory in the development of the hypothesis that girls' affective profiles can be influenced by single-sex verses co-educational learning environments. Cook and Reichardt espouse the view that research founded upon the aim of testing theory distinguishes it as quantitative in nature (cited in Evans 1994, page 320). Evans (1994) further suggests that this approach " tends towards determinism — based on forces (e.g. socialization), instincts, characteristics and/or attitudes." (page 320).
When research is explicitly driven by theory, the researcher's preconceptions have to be acknowledged as influential in the development and interpretation of this theoretical foundation. The feminist critique of research, as outlined by Damarin (1995), is recognized as valid when consideration is given to this investigation. This critique claims that the researcher and researched cannot be divorced from the environment in which they are enveloped; thus, any outcomes can be seen as socially meaningful and useful ways of interpreting a situation, rather than some form of objective reality. Damarin (1995), therefore, goes on to suggest, it is important that a critique of these outcomes is carried out with a view to understanding their relationship with the environment from which they were produced. As for any other research, this dissertation can be viewed as a product of an environment that is infused by sexism; thus, a critique from an objective external source would support the foundations upon which this investigation is built. Such a critique is both encouraged and welcomed.
Evans (1994) points out that "the quantitative approach is useful when we wish to make comparisons across . . . groups of subjects, and we aim for some degree of generality." (page 326). Such an approach, therefore, is suited to the central aim of this investigation, which is to ascertain a generalized view of the affective profile of girls who are educated in a single-sex school in Bermuda, and to determine whether or not this contrasts positively with the generalized affective profile of their female contemporaries who are being educated in a co-educational setting.
Such an approach has an inherent weakness, as Ernest (1994) points out, in that it can be insensitive to the individual student. In contrast, however, by selecting a large enough group of subjects, it is anticipated that a generalized view can be obtained, whereby any extreme affective profiles do not skew the results to such a degree that unreasonable claims with regard to the general situation are made.
Ernest (1994), also points out that:
All persons and human situations and contexts are unique and individual, but the scientific research paradigm requires that whole classes of individuals or events are regarded as identical, or at least indistinguishable in terms of a range of selected variables. Thus this approach can often be insensitive to contextual variations . . .
Ernest (1994, page 32).
In an attempt to reduce the errors associated with this approach, care has been taken in the selection of the co-educational school for participation in this study, although it has to be noted that this choice is limited by the fact that there are only ten such schools available in Bermuda. As outlined below, the co-educational setting which displays the greatest similarities in traits to the single-sex school has been chosen; however, it has to be acknowledged that it is not possible to eliminate all of the extraneous variables that may have an impact upon the affective profiles of the students. These variables may, for example, include social factors pertaining to the students, their attainment levels, and the attitudes of their teachers.
The Subjects of the Investigation.
The subjects of the investigation were drawn from two schools, both independent, with their own on-site feeder primary departments. The racial make-up of the student body of each school is approximately 60% white and 40% black. The schools have three forms at the entry level to their senior departments, each year group having a maximum capacity of sixty students. Acceptance into the secondary department is via an entrance examination, although the ability range in both schools is wide due to the relatively small population of school-age children in Bermuda, and the increasingly competitive market in independent schools. Students in both schools follow GCSE syllabi, most taking the examination at the end of their fifth year. PSAT and SAT examinations are also taken.
Attempts were made to obtain from the schools copies of results for the various public examinations, as this would have allowed for comparisons of achievement, as measured by these examinations; however, the administration of the co-educational school was not prepared to release these. It is perhaps understandable that in a small island community, data pertaining to the performance of any of the five independent schools tend only to be released in a manicured form for marketing purposes, an unfortunate situation as a lack of achievement data limits the comparative analysis of the two schools.
As was noted from the research literature, it has been hypothesized that some of the affective elements, particularly confidence, sex-role congruency, and the fear of success may be a function of age. Ideally, to obtain some insight into this area, a longitudinal study over several years would be of benefit; however, such an approach is impractical for this investigation. Thus, as Haladyna and Shaughnessy point out, "it seems reasonable and important to include several grade levels in any study of attitudes to determine if trends exist across grades." (quoted in Ma and Kishor 1997, page 43); hence, the use of two year groups was adopted to facilitate a comparison between the affective profiles of younger students and those of older students.
Secondary level students from Years 5 and 2 were asked to complete a questionnaire. It must, of course, be stressed that any conclusions drawn from a comparison between these two age groups will have to be treated with caution. It has to be acknowledged that the Year 2 and Year 5 five samples are unique and, therefore, any relationship may not be representative of any developmental aspect of the various affective components.
The choice of the Year 5 students was made, in particular, because they may have a more stable and well established view of both mathematics and of themselves as learners of mathematics, a view supported by the work of Ma and Kishor (1997). Additionally, their imminent participation in the important SAT and GCSE examinations makes insight into their affective profiles of particular value.
From the single-sex school, 49 Year 2 girls and 40 Year 5 girls provided data for the investigation, and from the co-educational school 35 Year 2 girls and 31 Year 5 girls provided data. A quantitative analysis of the data generated from these groups was used to address the main hypothesis of this study that girls educated in a single-sex environment display a more positive affective profile than their female contemporaries from a co-educational background.
Data were also obtained, however, from the boys in the same Year groups of the co-educational school to facilitate a cross-gender analysis of the affective profiles of the various groups; the Year 2 boys numbered 25 and the Year 5 boys numbered 22.
The Questionnaire.
A questionnaire (see Appendix 1) was used as the instrument to investigate the affective profiles of the students. As Smith (1975) points out, a primary strength of such an instrument is that it is one of the few techniques that allows for the collection of generalizable information pertaining to the study of attitudes, values, and beliefs.
Those components of the affective domain, discussed earlier, which have been hypothesized to be related to gender differences in the learning of mathematics form the foundation of this questionnaire. Questions related to the four components of confidence (C), the usefulness of mathematics (U), mathematics as a male domain (MD) and attitude toward success in mathematics (AS) were drawn from the Fennema and Sherman Attitude Scales (see Appendix 2).
These scales have been chosen because they were designed specifically to measure the attitudes pertaining to high school students; furthermore, they were developed in such a way as to establish content validity. Fennema and Sherman (1976) detail the steps that they took in this process. Each author wrote items independently and these were judged by the other author for validity. 173 items were agreed upon for the initial test and these were randomly distributed into one instrument. This instrument was administered to 367 students from grades 9 to 12, some of whom had elected to study mathematics, while others had not. Fennema and Sherman (1976) detail several criteria, in order of importance, that were used in selecting items to be included in the final version of the scales: these included those that correlated highest with the total score for each gender; those with higher standard deviations for each gender; those which yielded results consistent with the theoretical construct of the scale; and items that differentiated mathematics and non-mathematics students.
Six positive and six negative items were finally selected per scale, for which split-half reliabilities were calculated. The values of these reliabilities, for the scales utilized in this study, are given in Table 7.
Table 7: Split-half reliabilities, as calculated by Fennema and Sherman for their attitude scales.
SCALE |
SPLIT-HALF RELIABILITY |
| Attitude Toward Success (AS) | 0.87 |
| Mathematics as a Male Domain (MD) | 0.87 |
| Confidence (C) | 0.93 |
| Usefulness of Mathematics (U) | 0.88 |
Source: Fennema and Sherman (1976, page B4)
An independent construct validation study into the Fennema-Sherman Scales, using factor analysis, was also conducted by Broadbooks et. al. (1981). Their study, involving 1,541 junior high-school students, produced eight factors that they interpreted as empirical evidence to support the theoretical structure and measurement integrity of the scales. Similar results, also using factor analysis, have also been reported by Melanchon et. al. (1994).
Additionally, Eckard (1995) details the work of Hackett and Betz in which they also found the scales to be statistically reliable through the use of the Kuder-Richardson test. Their Kuder-Richardson values ranged from 0.86 to 0.90. (cited in Eckard 1995, page 25).
As can be seen from Appendix 2, each component scale consists of twelve questions, of which six reflect a positive affective profile and six reflect a negative affective profile. Students were asked to respond to each question using a graphic or Likert-type scale containing five response alternatives: strongly agree, agree, undecided, disagree and strongly disagree. Each response having a score of 1 to 5, the weight of 5 being allocated to the response that is hypothesized to have the most positive effect on the learning of mathematics.
One drawback of the Likert scale format which has to be recognized is the error of central tendency, whereby students may tend to opt to rate themselves near the centre of the scale rather than using the extremes. To help overcome this, administrators of the questionnaires were asked to stress the need for honesty and that strict confidentiality would be maintained. Such an approach may also have helped in reducing what Smith (1975) identifies as reactive error, whereby subjects modify their responses because they are being tested.
Questions 49 and 50 of the questionnaire relate to the attribution component (adapted from the Open University 1986, page 39). These have yielded usable data as questionnaire components in two previous investigations that I have carried out, the format seemingly posing no difficulty for the respondents.
A numerical representation of each response to the attribution question was based upon the hypothesis that, for success outcomes, internal and stable attributions contribute positively to the affective profile, whereas external and unstable attributions are neutral. In contrast, for failure outcomes, internal and stable attributions contribute negatively to the affective profile, whereas external and unstable attributions are neutral. This hypothesis is based upon the findings, reported by Seegers and Boekaerts (1996), of two meta-analyses of research into attribution, conducted by Whitley and Frieze, and Findley and Cooper. These analyses suggest that there is empirical evidence to show that success has a more positive impact when it is ascribed to an internal and stable cause (e.g. ability) and that failure has a less deteriorating effect when it is attributed to an external cause (e.g. bad luck).
Table 8 shows each of the attributions in terms of its positive, negative, or neutral contribution to the affective profile.
Table 8: Attributional impact upon student affective profiles for success and failure outcomes.
SUCCESS |
Internal |
External |
Stable |
Unstable |
Score |
Ability |
Positive |
Positive |
5 |
||
Effort |
Positive |
Neutral |
4 |
||
Task Difficulty |
Neutral |
Positive |
4 |
||
Luck |
Neutral |
Neutral |
3 |
FAILURE |
Internal |
External |
Stable |
Unstable |
Score |
Luck |
Neutral |
Neutral |
3 |
||
Task Difficulty |
Neutral |
Negative |
2 |
||
Effort |
Negative |
Neutral |
2 |
||
Ability |
Negative |
Negative |
1 |
As can be seen from the table, a score has been assigned to each attribution that equates with the five point scores allocated to the Likert scales used for the other affective components contained within the questionnaire. The scores for the success outcomes range from the positive value of 5 to a neutral score of 3; and for the failure outcomes, the scores range from a neutral value of 3 to a negative score of 1. Such a rating is based upon the assumption that success, however attributed, will not have a negative impact upon the affective profile and that failure will not have a positive impact.
Table 9 shows the range of scores available to the students when their attributions for success and failure are combined.
Table 9: Combined scores for success and failure attributions.
FAILURE OUTCOME
Ability |
Effort |
Task Difficulty |
Luck |
||
Ability |
6 |
7 |
7 |
8 |
|
SUCCESS |
Effort |
5 |
6 |
6 |
7 |
OUTCOME |
Task Difficulty |
5 |
6 |
6 |
7 |
Luck |
4 |
5 |
5 |
6 |
It has to be accepted that a numerical representation of the various combinations of student attributions for success and failure has its limitations; for example, one student ascribing luck to both outcomes obtains the same score as one ascribing effort to both outcomes. Consequently, consideration of just the numerical value ignores the implications of the different attributional styles of the students. However, this numerical approach does provide a single overall measure of attribution which allows for it to be integrated with the other four affective components to obtain a combined affective score for each student. The justification and methods adopted for this integration are given in the next section.
Analytical Methods.
The total affective profile scores provide a tool for analyzing holistically the impact of the five affective components as they work in combination for each group of students. Such an analysis addresses the central hypothesis of this investigation that girls' affective profiles, in general, are more positive if they are educated in single-sex environments. It also acknowledges that each affective profile is a multifaceted network of inter-related affective components, with no single component operating in isolation.
As Fennema and Sherman (1976a) point out, their attitude scales are designed to be used in any combination; however, to justify the inclusion of the attribution component, its correlation with the total score for the four other components has been assessed using Pearson's correlation coefficient (r). The details of this assessment are given in Appendix 3(ii).
The results indicate that a positive linear relationship exists between the total scores that students achieved on the four Fennema-Sherman components and the scores obtained for attribution. For the Year 5 girls from the single-sex school (SS5), the Year 5 girls from the co-educational school (CE5G), and the Year 2 girls from the co-educational school (CE2G), the degree of linear relationship was significant at the high level of 0.05%. For the Year 2 girls from the single-sex school (SS2), the degree of linear relationship was significant at the 1% level. For the boys, the level of significance was 5% for Year 2 (CE2B) and 0.5% for Year 5 (CE5B). It should be noted that the critical values for a 1-tail test have been utilized in this analysis, based upon the directional hypothesis that students displaying a more positive affective profile, as represented by their total scores on the Fennema-Sherman components, will also display a more positive affective score for attribution. Such a high degree of correlation suggests that the inclusion of the attribution scores with those for the other four components to obtain a total affective profile score for each student, may be justified.
When the scores for attribution are combined with those for the other components, the values obtainable for the total affective profile range from a maximum of 248 to a minimum of 52. The range of scores available on each of the four Fennema-Sherman scales is from 12 to 60; thus, a score of 36 can be considered as representative of a neutral affective position. As we have seen for attribution, a score of 6 reflects neutrality; thus, for the total affective profile, a score of 150 can be considered as neutral. Any score in excess of these neutral values is taken to represent a positive affective disposition; conversely, any score below these neutral values is taken to represent a negative affective disposition.
It has, of course, to be recognized that the structure of this affective network has been defined, for the purposes of this investigation, by those five components considered to be of major importance, as identified by the previous research; however, to suggest that such a structure is absolute would be unwise. It may be, for example, that various components become more or less important when viewed from a socio-historical perspective. The recent pervasive advances in technology may have had an impact upon beliefs pertaining to the usefulness of mathematics, for example.
It is important to understand the ways in which each of the affective components contribute to the total affective profile; thus, along with the quantitative analysis for the generalized affective profiles, comparisons between student groups were carried out for each of the affective components.
To facilitate this quantitative analysis, a set of descriptive statistics for each group of students has been calculated for each affective component of the questionnaire and for the total affective profile scores (see Appendix 3(iii)). The means generated by the two Year 5 groups of female students have been compared and, similarly, those generated by the two Year 2 groups of female students have also been compared.
Since the number of students (n) in each of these groups is sufficiently large, it can be assumed that the sampling distribution tends to be generally normal in form. This allows, therefore, the use of the normal deviate (z) to test hypotheses about the population means.
The significance test used was in terms of the test statistic:
z = x1 - x2 - (m 1 - m 2 )
� ( s 1� / n 1 + s 2� / n2)
where x1 = mean score for girls from the single-sex school.
x2 = mean score for girls from the co-educational school.
m 1 = population mean for girls from single-sex schools.
m 2 = population mean for girls from co-educational schools.
s 1� = population variance for girls from single-sex schools.
s 2� = population variance for girls from co-educational schools.
n 1 = number of girls in the sample from the single-sex school.
n2 = number of girls in the sample from the co-educational school.
Source: Crawshaw and Chambers (1984, page 481)
(Note that since the sample sizes were large enough, the sample variances were taken as estimates for the population variances).
For each component a 1-tail test was used based upon the general hypotheses:
H0 : m 1 = m 2 : with regard to the learning of mathematics, there is no difference between the affective scores for the girls educated in a single-sex environment and those for their female contemporaries who are educated in a co-educational environment.
H1 : m 1 > m 2 : with regard to the learning of mathematics, the girls educated in a single-sex environment have a more positive affective score than their female contemporaries who are educated in a co-educational environment.
In all cases, the value of z was considered for significance at the 5% level; however, where significance at either the 2% or 1% level are indicated, this has been noted.
Chapter 7: Results.
To facilitate an overview of the data obtained in this investigation, Figure 4 shows a box and whisker plot of the total affective profile scores for each group of students. The distribution of the maximum and minimum scores, the medians, and the interquartile ranges for each group can be discerned.
This section also contains details of the z-values for each affective component. Additionally, Figure 5 comprises of a series of graphs illustrating the distribution of the mean scores obtained by the various student groups on each component. The position of these means, relative to the neutral scores of 36 for the Fennema-Sherman scales and 6 for the attribution component, can be discerned from these graphs. The means for the total affective profile scores for all groups of students are in the positive range, i.e. greater than 150, as can be seen from Figire 5(vi).
Detailed results including the raw data for this investigation can be found in Appendix 3.
Figure 4: A box and whisker plot of the total affective profile scores for each group of students.
(i) Confidence (C).
Figure 5(i): Graph showing the distribution of the mean scores obtained on the
confidence scale by each group of students.
H0 : m 1 = m 2 : with regard to the learning of mathematics, there is no difference between the confidence levels of the girls
educated in a single-sex environment and those of their
female contemporaries who are educated in a co-educational
environment.
H1 : m 1 > m 2 : with regard to the learning of mathematics, the girls educated in a single-sex environment have more confidence than their female contemporaries who are educated in a co- educational environment.
Year 2: z = 2.271. (Since z > 2.054, H0 can be rejected at the 2% level of significance).
Year 5: z = 2.550. (Since z > 2.326, H0 can be rejected at the 1% level of significance).
(ii) The usefulness of mathematics (U).
Figure 5(ii): Graph showing the distribution of the mean scores obtained on the usefulness of mathematics scale by each group of students.
H0 : m 1 = m 2 : there is no difference in the perception of the usefulness of mathematics between the girls educated in a single-sex environment when compared with their female contemporaries who are educated in a co-educational environment.
H1 : m 1 > m 2 : the girls educated in a single-sex environment have a more positive perception of the usefulness of mathematics than their female contemporaries who are educated in a co- educational environment.
Year 2: z = -0.115. (Since z < 1.645, H0 cannot be rejected at the 5% level of significance).
Year 5: z = 1.471. (Since z < 1.645, H0 cannot be rejected at the 5% level of significance).
(A negative z-value indicates that the mean for the co-educated group is higher than that for the single-sex group).
(iii) Attitude toward success in mathematics (AS).
Figure 5(iii): Graph showing the distribution of the mean scores obtained on the attitude toward success scale by each group of students.
H0 : m 1 = m 2 : there is no difference in the attitude toward success in mathematics between the girls educated in a single-sex environment when compared with their female contemporaries who are educated in a co-educational environment.
H1 : m 1 > m 2 : the girls educated in a single-sex environment have a more positive attitude toward success in mathematics than their female contemporaries who are educated in a co-educational environment.
Year 2: z = 1.287. (Since z < 1.645, H0 cannot be rejected at the 5% level of significance).
Year 5: z = 0.980. (Since z < 1.645, H0 cannot be rejected at the 5% level of significance).
(iv) Mathematics as a male domain (M).
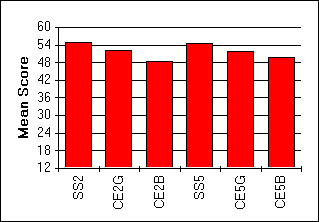
Figure 5(iv): Graph showing the distribution of the mean scores obtained on the mathematics as a male domain scale by each group of students.
H0 : m 1 = m 2 : there is no difference in perceptions pertaining to mathematics as a male domain between the girls educated in a single-sex environment when compared with their female contemporaries who are educated in a co-educational * environment.
H1 : m 1 > m 2 : the girls educated in a single-sex environment have more positive perceptions pertaining to mathematics as a male domain* than their female contemporaries who are educated in a co-educational environment.
Year 2: z = 2.144. (Since z > 2.054, H0 can be rejected at the 2% level of significance).
Year 5: z = 2.380. (Since z > 2.326, H0 can be rejected at the 1% level of significance).
(v) Attributional style.
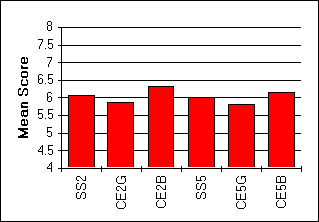
Figure 5(v): Graph showing the distribution of the mean scores obtained on the attribution scale by each group of students.
H0 : m 1 = m 2 : with regard to their successes and failures in mathematics, there is no difference between the attributional styles of the girls educated in a single-sex environment and those of their female contemporaries who are educated in a co-educational environment.
H1 : m 1 > m 2 : with regard to their successes and failures in mathematics, the girls educated in a single-sex environment have a more positive attributional style than their female contemporaries who are educated in a co-educational environment.
Year 2: z = 1.176. (Since z < 1.645, H0 cannot be rejected at the 5% level of significance).
Year 5: z = 1.124. (Since z < 1.645, H0 cannot be rejected at the 5% level of significance).
(vi) Total affective profile score.
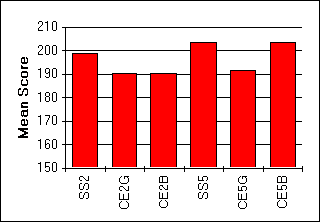
Figure 5(vi): Graph showing the distribution of the mean scores obtained on the total affective profile by each group of students.
H0 : m 1 = m 2 : with regard to their learning of mathematics, there is no difference between the affective profile scores of the girls educated in a single-sex environment and those of their female contemporaries who are educated in a co-educational environment.
H1 : m 1 > m 2 : with regard to their learning of mathematics, the girls educated in a single-sex environment have more positive affective profile scores than their female contemporaries who are educated in a co-educational environment.
Year 2: z = 1.777. (Since z > 1.645, H0 can be rejected at the 5% level of significance).
Year 5: z = 2.489. (Since z > 2.326, H0 can be rejected at the 1% level of significance).
The findings outlined above indicate that, where a significant difference has been found, it is consistently in favour of those girls from the single-sex school. Table 10 summarizes these findings.
Table 10: Significance levels for the differences between means for the single- sex educated girls' groups versus the co-educated girls' groups.
Year 2 |
Year 5 |
|
| Confidence | 2% |
1% |
| Usefulness | Not significant |
Not significant |
| Attitude to Success | Not significant |
Not significant |
| Male Domain | 2% |
1% |
| Attribution | Not Significant |
Not significant |
| Total Affective Profile Score | 5% |
1% |
As a follow-up to these findings, a similar analysis was carried out to compare the means generated by the girls' groups from the single-sex school and those generated by the boys from the co-educational school. Once again, a z-test was utilized, although this time a 2-tailed analysis was made based upon the general hypotheses:
H0 : m 1 = m 2 : with regard to the learning of mathematics, there is no difference between the affective scores for the girls educated in a single-sex environment and those of their male contemporaries who are educated in a co-educational environment.
H1 : m 1 � m 2 : with regard to the learning of mathematics, there is a difference between the affective scores for the girls educated in a single-sex environment and those of their male contemporaries who are educated in a co-educational setting.
From this analysis it was found that, where a significant difference was apparent, it was in favour of the female groups. Table 11 summarizes the results of this analysis.
Table 11: Significance levels for the differences between means for the single- sex educated girls' groups versus the co-educated boys' groups.
Year 2 |
Year 5 |
|
| Confidence | Not Significant |
Not Significant |
| Usefulness | Not significant |
Not significant |
| Attitude to Success | 2% |
Not significant |
| Male Domain | 1% |
1% |
| Attribution | Not significant |
Not significant |
| Total Affective Profile Score | Not significant |
Not Significant |
Similarly, the means generated by the co-educated girls were compared with their male peers. Once again, a 2-tailed z-test was utilized. Table 12 summarizes the results of this analysis. (Detailed results of all of the z-test analyses can be found in Appendix 3(iv)).
Table 12: Significance levels for the differences between means for the
co-educated educated girls' groups versus their male peers.
Year 2 |
Year 5 |
|
| Confidence | 5% in favour of boys |
1% in favour of boys |
| Usefulness | Not significant |
1% in favour of boys |
| Attitude to Success | Not significant |
Not significant |
| Male Domain | 5% in favour of girls |
Not significant |
| Attribution | 2% in favour of boys |
Not significant |
| Total Affective Profile Score | Not significant |
Not Significant |
These analyses have been included because they give rise to some interesting points for discussion; however, as will become apparent from the conclusions of this investigation, the appropriateness of cross-gender comparisons of affective profiles in general is open to question.
Patterns of Attribution.
As will be discussed in the next section, the mean scores for this component only partially reveal the construction of the attribution patterns for the various groups of students. A clearer picture emerges when consideration is given to the four attributions of ability, effort, task difficulty, and luck. Table 13 details the results from the questionnaire for each of these attributions.
Table 13: Distribution of the success and failure attributions for each group of students.
YEAR 2 |
SS2 (%) |
CE2G (%) |
CE2B (%) |
Difference (SS2 to CE2G) |
Attribution |
| SUCCESS | |||||
| Ability | 16 |
14 |
40 |
2 |
Internal/Stable |
| Effort | 53 |
66 |
44 |
-13 |
Internal/Unstable |
| Task Difficulty | 16 |
6 |
12 |
10 |
External/Stable |
| Luck | 14 |
14 |
4 |
0 |
External/Unstable |
| FAILURE | |||||
| Ability | 10 |
17 |
12 |
-7 |
Internal/Stable |
| Effort | 55 |
71 |
64 |
-16 |
Internal/Unstable |
| Task Difficulty | 20 |
9 |
16 |
11 |
External/Stable |
| Luck | 14 |
3 |
8 |
11 |
External/Unstable |
YEAR 5 |
SS5 (%) |
CE5G (%) |
CE5B (%) |
Difference (SS5 to CE5G) |
Attribution |
| SUCCESS | |||||
| Ability | 15 |
10 |
18 |
5 |
Internal/Stable |
| Effort | 65 |
77 |
64 |
-12 |
Internal/Unstable |
| Task Difficulty | 10 |
3 |
9 |
7 |
External/Stable |
| Luck | 10 |
10 |
9 |
0 |
External/Unstable |
| FAILURE | |||||
| Ability | 8 |
19 |
5 |
-11 |
Internal/Stable |
| Effort | 60 |
71 |
59 |
-11 |
Internal/Unstable |
| Task Difficulty | 30 |
10 |
27 |
20 |
External/Stable |
| Luck | 3 |
0 |
9 |
3 |
External/Unstable |
The contents of this chapter represent a summation of the main results obtained from this study. These will be discussed in the next section.
Chapter 8: Discussion of the Findings.
To facilitate this discussion, consideration will initially be given to the total affective profile scores and then to each affective component.
(i) The total affective profile scores.
The data suggests that the Year 2 girls educated in a single-sex environment have a significantly more positive total affective profile score (x=198.92) than do their co-educated female peers (x=190.11), as defined by the five selected components. Two particular components, those of confidence and mathematics as a male domain, contribute significantly to this more positive profile. It should be noted that lower scores on the mathematics as a male domain scale indicate a greater acceptance of the view that the subject is androcentric in nature; thus, higher scores on this scale are perceived as contributing positively to the affective profile.
One unique element contained within the data pertains to the mean score for the Year 2 co-educated group of girls (x=46.23) which surpasses that of their single-sex educated peers (x=46.02) on the usefulness of mathematics scale, although not significantly. On all of the other components, for both year groups, the mean scores for the single-sex groups are consistently higher, although, once again, not always significantly so.
An interesting similarity exists between the results obtained from the Year 2 students and those in Year 5. As for the younger students, the Year 5 girls educated in the single-sex environment appear to have a more positive total affective profile (x=203.83) than do their co-educated peers (x=191.84); additionally, the degree of significance is at the higher level of 1%. Once again, the major contributory components to this difference are those of confidence and mathematics as a male domain.
An insight into the structure of the total affective profile for each group of students is revealed when consideration is given to the mean scores obtained on each component when compared with the neutral score on each scale. The means obtained by the Year 2 single-sex group all fall within the positive range. This is also true for the Year 2 co-educated girls, except on the attribution component. The pattern for the Year 5 groups of girls replicates that of the younger students with the sole exception of a mean attribution score of 6 for the single-sex group which suggests neutrality.
As can be seen from Figure 6 below, when consideration is given to the group means, the degree of positivity across the five components follows the same pattern for all of the girls' groups. Following attribution as the least positive component is confidence, then the usefulness of mathematics, attitude toward success and, finally, the most positive component appears to be the rejection of the view of mathematics as a male domain. Interestingly, all but three students in the survey obtained positive scores on this final component: one Year 2 girl from the single-sex school and two Year 5 boys.
It should be noted that the attribution means have been scaled to allow for a common axis in Figure 6, whereby the minimum score of 4 on the attribution questions translates to a minimum score of 12 on the Fennema-Sherman scales, and a maximum of 8 for attribution translates to a maximum of 60 on Fennema-Sherman. Thus, a neutral score of 6 for attribution translates to the neutral score of 36 on the scales for the other four components.
Figure 6: Graph showing the distribution of the mean scores obtained by each group of students across all affective components.
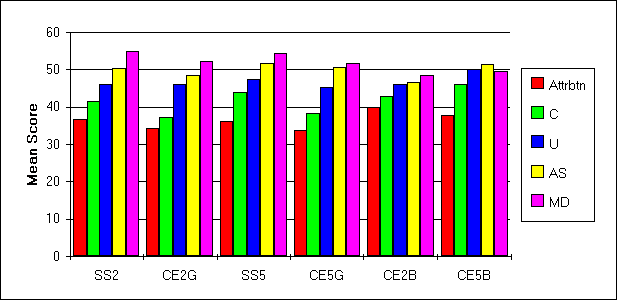
It should be noted that caution has to be taken in interpreting this pattern, as it may be a result of the structure of the questionnaire. In particular, the different style of the attribution questions, when compared with those of the other four affective components, could be discriminatory. Such caution is reinforced by the fact that the data for the Year 2 boys' group also follows the same pattern as the girls' groups. It is interesting to note, however, that, for the older boys, the mean score on the component of mathematics as a male domain is relegated below those obtained on both the usefulness of mathematics and the attitude toward success scales.
(ii) Mathematics as a male domain.
It appears that beliefs concerning the androcentric nature of mathematics are central to the differences in the data obtained by the various groups. For both age groups, the means obtained by the girls from the single-sex school were higher than all other groups, at the 1% level of significance, except for the Year 2 co-educated girls, at which the level of significance was 2%. Whilst the co-educated girls' groups had mean scores that were higher than their male peers, only that for the younger students was significantly higher, at the 5% level. Such a situation appears to support the view that, for girls, a single-sex environment may result in a more positive view of mathematics as an appropriate area of study for females.
It has to be recognized that the classroom situation is an agent of socialization that includes the dynamics of gender. Spender (1982) suggests that in mixed classes girls submit to the learned dominance of boys. She argues that for these girls education tends towards indoctrination and an exercise in the art of subordination. Thus, with regard to mathematics as a male domain, it is possible to speculate that the boys in the study, who are not so positive in regard to girls' participation in mathematics, may have a negative impact upon the opinions of the girls who share their classrooms. Such speculation is supported by the views of Koehler and Fennema (1982) who state that "since boys, much more than girls, stereotype mathematics as a male domain, they no doubt send many subtle, and not-so-subtle, messages that girls who achieve in mathematics are somehow less feminine." (page 103).
Morrow and Morrow (1995) advocate segregation as a way of freeing girls from such oppressive situations. As Mura (1995) points out, "this argument proceeds from a radical feminist standpoint which analyses classroom interactions in terms of oppression and dominance, and aims at girls' autonomous development without reference to boys. It claims neither equality nor difference." (page 158).
It was noted earlier that beliefs pertaining to mathematics as a male domain may be a function of age; as girls become more aware of their gender-role, their views on the suitability of pursuing the study of mathematics might diminish. The results from this investigation may support such a view; the mean scores for both Year 5 groups of girls (SS5, x=54.53; CE5G, x=51.77) are lower than those for their counterparts in Year 2 (SS2, x=54.98; CE2G, x=52.23). Interestingly, these results have arisen despite the fact that the co-educated Year 5 girls are accompanied by boys who have a more positive regard for girls' participation in mathematics than do their Year 2 male counterparts. Such an apparent anomaly goes some way to repudiate the argument, espoused above, concerning the negative influence of boys in mixed classes. It may be that the views of younger boys, however, do not have such a great influence on the younger girls, who are less aware of their gender-role.
Despite the lower scores on the mathematics as a male domain component for both groups of Year 5 girls, it should be noted that the differences in the significance between the means for the single-sex group and the co-educated group is greater for these older students. Once again, this lends support to the view that, for the sample studied, the single-sex environment has been of affective benefit within this domain.
It is possible to speculate that the culture of the single-sex school may have a positive impact upon the girls' attitudes towards mathematics. There appears to be a constant reinforcement of the message that the students can be successful, not only as learners, but specifically as female learners in all areas of study. This message is transmitted by the teachers, administrators, counsellors, and the many outside speakers who are brought in with this purpose in mind; in this way, the single-sex setting appears to provide a forum for the unfettered promotion of the success of girls.
In addition, good teachers of mathematics will be consistently informing their students, whether they be in co-educational or single-sex classes, that they can be successful in the subject. Unless this message is reinforced on an individual basis, however, the girls in co-educational classes may interpret this as more applicable to their male peers, particularly if they subscribe to the androcentric view of the subject. No such option exists for those in single-sex environments; thus, mathematics as a female domain is promoted.
Thompson (1995) extends this argument when she states that, "in single-sex environments, female students are forced to assume leadership roles and develop co-operative networks. They cannot 'bow out' of difficult problems leaving them to the boys and so have to take the lead and solve problems for themselves." (page 28). Such a situation sends a powerful message to the girls involved as it pertains to the expectations of their engagement in mathematics. Ernest and Bayliss (1995) point out that, as such expectations become internalized as student expectations, they have a profound effect upon mathematical self-concept and perceptions of self-efficacy.
(iii) Confidence.
The argument outlined above, pertaining to the significantly higher scores for the single-sex educated girls on the component of mathematics as a male domain, may, at least in part, be related to their scores on the confidence component. If these girls, like their male contemporaries, are receiving and internalizing a message pertaining to their positive engagement in the study of mathematics, then an accompanying increase in their level of confidence may also be expected. Such a view appears to be supported by the data; the mean scores for the single-sex educated girls on the confidence component are significantly higher than those of their female co-educated contemporaries, at the 2% level for the Year 2 students and at the 1% level for the Year 5 students. In addition, the higher confidence scores for the single-sex educated girls are not significantly different from those of the co-educated boys, although, at both year levels, the boys' mean confidence scores are higher (SS2, x=41.45; CE2B, x=42.68; SS5, x=43.88; CE5B, x=46.09).
The median mark of 35 for the Year 2 co-educated girls on this component is unique amongst the various sub-groups, in that it represents a negative affective score; i.e. less than 36. Only 46% of these students obtained scores within the neutral or positive zone of confidence. The Year 5 co-educated girls' group appears to be more positive in regard to this component, with 61% gaining neutral or positive scores. All of the other groups, however, surpassed the co-educated girls: 68% of the Year 2 co-educated boys, 76% of the Year 2 single-sex educated girls, 80% of the Year 5 single-sex educated girls, and 86% of the co-educated boys scored in the neutral or positive zone for confidence.
When consideration is given to the generalized research findings that self-confidence has a stronger correlation with attainment than with any other affective variable, then the results obtained in this study raise concerns with regard to this component for the co-educated girls.
(iv) The usefulness of mathematics.
Relative to confidence, the perception of the usefulness of mathematics appears to be higher for all groups, and no significant differences are apparent between the means for the single-sex and those for the co-educated groups of girls. This may have positive implications for motivation; if mathematics is valued for its utility, then the students may have a tendency to persevere with their work in the subject, and this might occur despite a lack of confidence in some students.
A comparison of the data on the usefulness of mathematics for the two sets of girls' groups does not necessarily reveal the whole picture with regard to this component. Whilst there is not a significant difference between the single-sex girls' groups and the boys' groups, when the mean score for the Year 5 co-educated girls is compared with that for their male peers, it is found to be significantly lower at the 1% level. This situation may suggest that the single-sex educated girls are at least approaching a similar level of perception to that of their male contemporaries with regard to the utility of mathematics; however, the co-educated girls continue to reflect the more generalized research findings which indicate that females report a lower perception of the usefulness of mathematics. Such a finding gives rise to further concerns with regard to the affective profiles of these co-educated girls.
(v) Attitude toward success.
No clear picture emerges when consideration is given to the scores obtained on the attitude toward success scale. One scenario may be suggested by a comparison of the girls' groups; however, this is not necessarily supported when consideration is given to the scores obtained by the boys' groups.
If the girls' groups are considered, the scores obtained on the attitude toward success scale appear to challenge the theorized linkage between this component and that of mathematics as a male domain. If the source of a fear of success is the individual's loss of her sense of femininity, then those females subscribing to a more androcentric view of mathematics should theoretically have a more negative attitude to success within the subject. Conversely, the single-sex educated girls, who appear to be significantly more positive in their rejection of mathematics as a male domain, could be expected to surpass their co-educated counterparts on the attitude toward success component; however, no significant difference at either year level is apparent.
This situation gives rise to an interesting question with regard to the foundation of the belief that mathematics is a suitable area of study for females. Could it be that there is some conflict between an objective-based recognition that mathematics is not gender specific and the more subjective view that maybe it really is androcentric? Are the girls receiving mixed messages which are leading to a degree of affective dissonance? It may be that the single-sex educated girls, in particular, are in a position of what Isaacson (1989) terms as double conformity, whereby they are faced with the dilemma of having "to conform at the same time to two sets of standards or expectations, where these two sets are mutually inconsistent." (page 191). These expectations pertain to girls as learners of mathematics, in contrast to others related to their femininity.
For the single-sex educated girls, it has been speculated that the culture of their school relates and reinforces the view that mathematics is for them as females; this is the message that these girls suggest through their answers to the questions on the mathematics as a male domain scale. However, as Willis (1995) states:
To suggest or imply that girls have a 'free (unconstrained) choice' to be and do anything, and that their 'disadvantage' can be overcome by changes in their individual attributions or choices about mathematics is . . . dishonest and possibly even cruel.
Willis (1995, page 187).
In attempting to keep the message simple, it may have become simplistic, and in reality many of the girls fail to be persuaded. Had the message been genuinely accepted, then an accompanying increase in the single-sex educated girls' scores on the attitude to success scale could have been anticipated. A lack of evidence in this regard, however, might suggest that the girls are returning the message that, in reality, the choices they make cannot be devoid of the gender-imposed constraints that encompass them. Willis (1995) summarizes this situation when she states:
We are quite often exasperated when we try to convince girls that they can be engineers and they persist in missing the point and asking who is going to tuck in the baby. When we tell them they can do anything, they suspect we mean that they are expected to do everything.
Willis (1995, page 188).
The interpretation of the results given above may imply that powerful norms impact upon girls as gendered learners. It would be unreasonable, however, to make such a claim without reference to the results obtained by the boys' groups. If, as has been suggested, the apparent anomaly between the single-sex educated girls' scores on the mathematics as a male domain scale and the attitude toward success scale is due to their fear of a loss of femininity, then it could be expected that the boys' scores for attitude toward success would be higher; however, this is not the case. At the Year 2 level, the mean score for the single-sex educated girls is significantly higher than that for the boys (SS2, x=50.41; CE2B, x=46.6). No significant differences are evident between any other groups.
Such findings appear to contradict the interpretation of the results for the comparisons between the scores for the girls' groups. It may be that a positive interpretation of the girls' scores on the attitude to success scale is appropriate because they are at least equivalent to those of their male contemporaries, who are not constrained by expectations pertaining to femininity, but such an interpretation is one directional in nature. It may be that there are gender-specific factors, not revealed by the results, that act as constraints for the boys in the study; thus, a negative interpretation of their scores might be more appropriate. In turn, similar scores by the girls' groups, with the exception of those from the Year 2 single-sex environment, could also be viewed as negative.
It is quite apparent that no clear interpretation of the scores obtained on the attitude toward success scale emerges from the analysis outlined above. Insight into whether or not the scores for the various groups can be viewed as relatively positive or negative needs to be determined. Such insight can only be sought through further investigation.
(vi) Attribution.
The attribution component makes the least positive contribution to the total profile of all groups of students; however, several interesting points emerge from the data. When consideration is given to the mean scores, those obtained by both groups of co-educated girls fall into the negative zone (CE2G, x=5.86; CE5G, x=5.81). The Year 5 single-sex group mean represents neutrality (x=6) and that obtained by the Year 2 single-sex group falls fractionally within the positive zone (x=6.06). These slight increases for the single-sex groups cannot be seen as significantly higher than those of their co-educated peers.
Only 14% of the Year 2 co-educated girls have positive scores on this component, compared with 20% of the Year 2 single-sex educated girls and, interestingly, 44% of the Year 2 boys. For the Year 5 students, 10% of the co-educated girls, 18% of the single-sex educated girls, and 18% of the boys achieved positive scores.
One aspect of this data supports the more generalized research findings, in that the boys have surpassed both sets of girls' groups on this component. In particular, when the mean score for the Year 2 boys' group is compared with that obtained by their female classmates, a significant difference, at the 2% level, is found.
Further insight into this component is provided by the distribution of the success and failure attributions for each group of students, detailed earlier in Table 13. When consideration is given to the students' attributions for success, it can be seen that the girls' and the boys' responses comply with the research findings, illustrated in Table 6. Irrespective of the environment in which they are educated, the majority of the girls cite effort as their attribution for success. This is also true for the boys, but they cite ability for their success in greater numbers than the girls, particularly at the Year 2 level. The number of girls attributing success to ability is relatively small, although there are slightly more from the single-sex groups at both year levels. By attributing their successes to effort, the girls may generate feelings of pride; however, they might lose out on the feelings of competence that the boys may also generate when attributing their successes to ability.
Interestingly, upon completing the questionnaire, one Year 5 girl from the single-sex group made the unsolicited comment that she felt that it would be "conceited" to claim that one's success was due to natural ability. Whether or not such a sentiment is prevalent, particularly amongst girls, despite the assurance of confidentiality, is open to question. If this were found to be the case, however, it could be indicative of the constraining nature of gender-related norms as they pertain to girls. This may, in turn, impact upon the data with regard to the number of girls prepared to cite ability as an attribution for their success. Of course, a similar argument could also be made on behalf of the boys.
The high proportion of girls citing effort as their attribution for success may contribute positively to their affective profiles. If the students perceive their efforts to be typical, then future success can be expected. Similarly, if they are considering their effort related to specific tasks at which they have been successful, then they have the advantage of control; if they choose to repeat such an effort, then they can still expect success.
While the slight increase in the attribution of ability for success amongst the girls' groups seems to favour those from the single-sex environment, the converse is found when consideration is given to the attribution of task difficulty. Although the numbers are small, an increase in the citing of this attribution can be discerned for both year levels of the single-sex groups. For these girls, the perception that their success is due to the easiness of the work may not lead to an enhancement of their self-esteem; thus, no positive contribution to their affective profiles could result. Such a situation may also be true for the boys who cite task difficulty for their successes at similar levels to those of their single-sex educated female peers.
The attribution of a lack of effort to failure outcomes is substantial for all of the groups, particularly those of the girls from the co-educational environment. Such an attribution can be considered as neutral, in that the expectancy of future success does not decrease.
More of the co-educated girls cite the ability attribution for a lack of success, particularly in Year 5. Such an attribution may have a negative impact upon their affective profiles, in that feelings of ineptitude and shame can be generated, feelings which tend to impair motivation, and, in turn, may limit student attainment.
While the attribution of ability to failure outcomes may discriminate against the co-educated girls, the higher levels of attribution of task difficulty by the single-sex educated girls' groups and the boys' groups may have a more positive impact upon their profiles. Ability differs from task difficulty in terms of its locus of causality; by attributing their lack of success to the external component of task difficulty, the single-sex educated girls and the boys in the study may be avoiding the detrimental aspect of internalizing in this situation. As Paulos (1988) states:
Some people personalize events excessively, resisting an external perspective, and since numbers and an impersonal view of the world are intimately related, this resistance contributes to an almost willful innumeracy.
Paulos (1988, page 80).
In addition, by attributing their lack of success to impersonal factors, these girls and boys may limit any negative impact upon their self-esteem.
As with lack of ability, task difficulty is stable; therefore, some similar outcomes may be expected, particularly with regard to student motivation. As Kloosterman (1988) points out, "attributions to stable causes have a greater influence on students' motivation than do attributions to unstable causes because the student can expect stable causes to result in similar amounts of success or failure in the future." (page 346). Thus, lower motivation may be expected from elements of both the co-educated groups and the single-sex educated groups of girls, due to their respective choices of ability and task difficulty for failure outcomes. For both attributional styles, effort cannot be called upon to overcome unchanging causes of failure.
In terms of motivation, then, these different attributional levels for ability and task difficulty do not seem to favour girls from either the co-educational or the single-sex environment. Nonetheless, a lack of motivation might be particularly detrimental to girls in general, in that the combination of environmental and learner-related variables, discussed earlier, may be working to discriminate against their endeavours to learn mathematics. As Hensel (1989) suggests, "Only those females with high self-confidence and motivation to learn mathematics are able to withstand these pressures." (page 650); thus, when the co-educated girls' tendency to attribute failure to potentially de-motivating stable causes is seen in combination with their lower confidence profiles, a less favourable situation emerges for these students.
Summary of the Main Findings.
In general, all of the groups in this study have obtained positive affective profile scores; however, the scores for the single-sex educated girls' groups appear to indicate that they have more positive affective dispositions with regard to their learning of mathematics, when compared with the girls from the co-educational environment. Confidence and a rejection of the view of mathematics as a male domain appear to be the major contributory components to this difference. Variation between the single-sex educated girls and the co-educated girls is more significant for the older students.
No significant differences between the total affective profile scores are apparent for any of the other groups in the study, although differences do appear to exist on some components. Differences between the single-sex educated girls and the boys, favour the girls on the mathematics as a male domain component at both year levels and the attitude to success scale for the younger students.
The co-educated girls' confidence scores are significantly lower than their male classmates, as they are for the scores on the usefulness of mathematics scale in Year 5 and for attribution in Year 2. The co-educated girls, however, do score higher than their male peers on the mathematics as a male domain scale.
The degree to which each of the five components contributes to the affective profiles follows the same pattern for all of the girls' groups; attribution is the least positive, followed by confidence, the usefulness of mathematics, attitude toward success and, finally, a rejection of the view of mathematics as a male domain makes the most positive contribution.
Results from the single-sex groups may indicate that a more positive view of mathematics as a suitable area of study for females is linked with a higher degree of confidence in the subject.
The perception of the usefulness of mathematics amongst the single-sex educated girls approaches that of their male contemporaries; however, this is not the case for the older co-educated girls.
The increased perception of mathematics as a suitable area of study amongst the single-sex educated girls is not supported by a significant increase in their scores on the attitude to success component. This may indicate a degree of affective dissonance derived from a contrast between the messages being received by these girls in their school environment and those being received from wider society, as they pertain to beliefs about mathematics as a suitable area of study for females. The scores for all of the girls' groups on the attitude to success component, however, are at least equivalent to those obtained by the boys. If, as has been theorized in the research literature, boys are not inhibited by negative consequences associated with success, then from this perspective the equivalent scores obtained by the females could be viewed as positive. Furthermore, these scores do not appear to have been affected by either the educational environment or the girls' views concerning mathematics as a male domain because there is no significant difference between the girls' groups.
An interpretation of the attitude toward success scores is obscured further if consideration is given to the possibility that the boys' scores may have been adversely affected by unidentified factors that have had a negative impact. Such a scenario would not enable a positive interpretation of the girls' scores through their equivalence with those of the boys.
No clear interpretation of the scores on the attitude toward success scale emerges; thus, this appears to be an area that lends itself to further investigation.
Although no significant difference is found between the mean attribution scores, those obtained by the co-educated groups of girls fall within the negative zone; thus, the attribution patterns that these girls are displaying may have a detrimental impact upon self-esteem and motivation, which, in turn, may limit attainment.
For success outcomes, the positive attribution of effort is cited by most girls, irrespective of age or educational environment; thus, feelings of pride may be generated. However, more of the boys in the study attribute ability for success; thus, along with pride, feelings of competence may also be generated. For the girls' groups, a small increase in the more positive attribution of ability, cited by those from the single-sex environment, may be favourable; however, a similar increase in the number of single-sex educated girls citing the more negative attribution of task difficulty as a cause for success may not result in an enhancement of their self-esteem, due to its external nature.
For failure outcomes, the attribution of lack of effort is cited by most girls, irrespective of age or educational environment. This can be considered as neutral, in that it does not decrease the expectancy of future success; however, the greater number of co-educated girls who cite a lack of ability for failure outcomes could be unfavourable. The internal and stable nature of ability, when applied to a lack of success, can act to de-motivate, particularly when combined with lower levels of confidence. In contrast, a small increase in the attribution of task difficulty for failure outcomes, cited by the single-sex educated girls, may not be as unfavourable as ability due to its external nature, although its stability may still act to impair motivation.
Chapter 9: Conclusions and Recommendations.
It is impossible to separate the cognitive from the affective domains in any activity . . . . The most important is that there is a cognitive component to every affective objective and an affective component to every cognitive objective.
Maker (quoted in Ma and Kishor, 1997, page 26).
The view espoused by Maker is central to this investigation, in which the results suggest that, for the students studied, the affective profiles of girls from the single-sex environment appear to be more positive than those of the co-educated girls, as they pertain to the learning of mathematics. Similarly, the co-educated boys' scores surpass those of their female classmates on several affective components. Additionally, the scores for the single-sex educated girls are at least equivalent to those of the co-educated boys. These results give rise to several related questions. What can be learned from the results? What are the implications for the students in this study? How does this work relate to current thinking in the field of gender differences in mathematics? If the claims for the alignment of this investigation with the critical theoretic research paradigm are to be substantiated, how do we proceed to improve the provision of mathematics education in Bermuda, based upon the findings?
Before moving on to address some of these questions, it is important to recognize that the results are a product of an investigation that may well have been subject to several methodological weaknesses. The limited choice of schools for comparison in Bermuda may have been of particular detriment. Furthermore, the importance of the variations that exist between the contextual situations from which the data have been drawn may have been diminished by the quantitative analysis that has been adopted. As Ernest (1994) points out, such an approach can lead to simplification and the unquestioning of assumptions. Variations between the schools may relate to such factors as student achievement, social factors pertaining to the students, the culture of the schools involved, selectivity bias of the parents, and the nature of the delivery of mathematics education in the schools. Undoubtedly, an attempt to incorporate controls for these factors would have strengthened any claims for the validity and reliability of the data.
Similarly, a longitudinal study would have strengthened the data pertaining to patterns of affect and achievement over time. The two year groups used in this study are unique; thus, any suggestion that the data is representative of developmental changes has to be treated cautiously.
The instrument used in this investigation and the analytical methods adopted for the data that it provided may also be subject to weaknesses. The five components used to define the affective network have been drawn from an analysis of the recent research literature; however, the fallibility of such a definition is recognized. In addition, the integration of the attribution component with the more established Fennema-Sherman Attitude Scales may not necessarily provide a reliable measure for the total affective profiles. Reactive and central tendency errors, associated with Likert-type scales, are also acknowledged as weaknesses that may have impaired the results.
Attempts have been taken to limit errors associated with the factors outlined above; however, whilst elimination is desirable, it may not necessarily have been feasible.
It should to be reiterated that in global terms, the populations used for this investigation are very small; thus, it would be unwise to draw any generalized conclusions. The local significance becomes more apparent, however, when consideration is given to the fact that the students from the all-girls school represent all of the girls within their age range who are educated in a single-gender environment in Bermuda.
It has been argued, with the support of the research literature, that a more positive affective disposition towards mathematics leads to higher achievement in the subject. Unfortunately, no evidence is available at this time to substantiate this claim as it pertains to the students in this study. To seek such evidence would be a natural extension of this investigation; however, the reluctance of schools within the very small community of Bermuda to release results for comparative study would initially have to be overcome.
Irrespective of the absence of a quantifiable analysis of the relationship between affect and achievement, several important conclusions can be drawn from the findings.
(i) Poor affective dispositions amongst girls cannot be viewed as being
merely a product of their gender.
It is clear that the quantitative analysis carried out in this investigation can only be viewed as a starting point for further study; however, it is perhaps pointing us in the right direction by indicating that poor affective dispositions associated with girls and their study of mathematics cannot be assumed to be simply a product of their gender. The evidence to support this claim is illustrated by the affective profile scores of the girls educated in a single-sex environment. Not only do these scores surpass those of the co-educated girls, but they are at least equivalent to those of the co-educated boys. If some groups of girls have positive affective profiles, then there has to be something beyond gender that is preventing other groups of girls from achieving similar dispositions.
(ii) When consideration is given to the affective profile scores of girls, the
more positive affective disposition of the single-sex educated girls should
become the point of reference: a deficit view of girls' affective profiles is
neither appropriate nor productive.
Kaiser and Rogers (1995) suggest that much of the research into gender differences and mathematics carried out in the 1980s had the intention to value and affirm girls and girlhood but fell short. Often, differences were emphasized in a form that negatively compared girls to boys, women to men. In doing so, Willis (1995) contends that:
We perpetuate certain ways of viewing females and males which undermine girls and women. . . . Male skills and attributions are seen as the norm against which females become the negative other — to become equal is to become male.
Willis (1995, page 187).
The results of this survey may suggest that a deficit view of girls is inappropriate. Where significant differences exist, the single-sex educated girls in the survey surpass their male contemporaries, on the mathematics as a male domain scale in both year groups and on the attitude to success scale for Year 2. Furthermore, the significantly higher total affective profile scores obtained by the single-sex educated girls, when compared with those of the co-educated girls, suggests a more positive affective disposition as it pertains to the learning of mathematics. In particular, greater confidence and a rejection of the view that mathematics is a male domain appear to be major contributory components to this more positive affective disposition. Such a situation may suggest that the affective profiles of the single-sex educated girls in the survey should become the point of reference. Further analysis of this disposition and its relationship with the school context from which it has been derived may lead to pedagogical insights that can improve the mathematical learning for a wider range of students.
Interestingly, such an approach reflects a general trend in the research being carried out in the field of gender and mathematics. Kaiser and Rogers (1995) suggest that this research is moving away from seeing women as victims or as problems in mathematics, to one that considers women as central to the development of mathematics. They further assert that pedagogical processes are in a transitional stage, whereby consideration is given to "the experiences of women central to their mathematical development, and in which emotion and reason play balanced roles." (page 8). Such a shift can be seen in terms of one that moves from the negative domain of disempowerment to one of empowerment.
However, caution needs to be taken that such an approach does not merely replace one gender-specific perspective with another. Such a perspective is evident when methods that have been successful for some groups of boys are applied to some groups of girls without any adaptation to their needs and circumstances. Any practices arising out of contemporary analysis will have to improve the study of mathematics for all students.
(iii) The affective profile scores of the co-educated girls give rise to
concern.
It would be inappropriate to make the argument that a single-sex environment is always best; however, such an environment does appear to serve the young women in this survey well, as it pertains to their mathematics-related affective profiles. Concerns arise with regard to those girls who are being educated in the co-educational environment. Undoubtedly, the question of why these girls appear to have a reduced level of confidence, a less positive view of mathematics as suitable for study by females, and a weaker affective profile in general has to be addressed.
(iv) The lower scores obtained on the confidence component by the co-
educated girls in this study may be of particular detriment to their
success in mathematics. Greater insight into the causes of these scores
needs to be sought.
Some of the research literature discussed earlier suggests that the classroom experience for co-educated girls in particular can act as an agent of wider social expectations of them and that these impact negatively upon their confidence levels. It may be that such an interpretation is appropriate for the results of this investigation; however, it must be acknowledged that, at this time, this view is highly speculative because the results have been drawn from a minimal data set from only two schools. Thus, apparent differences could be a result of contextual differences other than the gender composition of the classes.
Clearly, further investigation is required in an attempt to understand the causes of the lower confidence levels that are apparent amongst the co-educated girls. Through this understanding, steps may be taken to enhance confidence levels, which would appear to be of particular importance when consideration is given to the conclusion of Kloosterman (1988) that this component has a stronger correlation with achievement than any other affective variable. In addition, if, as Walden and Walkerdine (1986) contend, it is necessary to possess the confidence to challenge the rules of mathematical discourse for real understanding to take place, then it important that girls reach this level of confidence, irrespective of their educational environment.
(v) This investigation gives rise to a requirement of further research.
As can be seen, the results of this investigation have generated several questions with regard to the mathematics-related affective profiles of girls and their mathematics education in general. An attempt has been made to address some of these questions with reference to various theoretical perspectives and the research findings documented in the literature; however, it is recognized that the conclusions are open to debate and contain a degree of speculation. To facilitate greater understanding, therefore, further research is required. The view of Fennema seems particularly appropriate in this case, when she states:
An understanding of gender and mathematics derived [only] from studies done from [a positivist] perspective will be limited. We will not deepen our understanding of gender and mathematics until scholarly efforts conducted in a positivist framework are complemented with scholarly efforts that utilize other perspectives [for example, from cognitive science and feminism].
(Quoted in Kaiser and Rogers, 1995, page 9).
The results of this investigation could certainly be enhanced and extended through such analyses. Insight into the ways in which the classroom experience contributes to the construction of student attitudes may be forthcoming. In addition, the direction in which girls' attitudes move, through the provision of a single-sex or a co-educational environment, requires further examination. If, as has been suggested, the profiles of the single-sex educated girls are held up as the reference point for all girls in the survey, then are we justified in concluding that the co-educational environment is having a negative impact upon girls? To draw such a conclusion seems to be supported by the confidence findings and much of the more generalized research; for example, Leder (1990b), Orenstein (1994), Campbell (1995), and Sadker and Sadker (1994).
The view that the co-educational classroom can lead to affective impairment has serious implications for the girls in the survey who are being educated in such an environment. An argument could be made for extending the provision of single-sex education, at least until a more equitable situation prevails for girls in co-educational settings.
If the teachers of Bermuda can address these and related issues, then we may be in a stronger position to help enhance the provision of mathematics education. If, for example, we are able to determine what components of the single-sex environment maintain, or generate more positive attitudes, then the lessons learned may be applicable within the co-educational situation. It might be that single-sex provision should become an option for mathematics classes in the co-educational schools, although the implications for the male students could not thereby be ignored. It has to be acknowledged, however, that current data is insufficient to make firm recommendations.
Clearly, further research is required to determine whether or not the reduced affective profile scores of the co-educated girls are a result of the classroom environment, and if so to what degree. If a correlation is found, then the components that contribute to a detrimental situation for these girls need to be investigated and, more importantly, acted upon.
It may also be inappropriate, if not impossible, to consider the role of the classroom experience in isolation. In attempting to interpret the results of this study, several speculative references have been made to the possible impact that factors external to the classroom may have had upon the affective scores of the various sub-groups. This is illustrated by the apparent incongruency between the results on the mathematics as a male domain and the attitude toward success components for the single-sex educated girls. Could it be that the attempts made by the single-sex school to convince their students that mathematics is for them as girls has little real impact upon the contrasting messages that they are receiving from wider society?
Similar questions arise when an explanation of the cross-gender results on the attitude towards success scale are sought. If the results contained in the study were replicated in wider contexts, would it be appropriate to view the girls' scores as positive, in that they are at least the equivalent of those of the boys? If so, is there any evidence to suggest that forces external to the classroom are reinforcing the view that success in mathematics is not in some way the antithesis of femininity? Further investigation may, however, produce evidence of a contrasting nature. Should the boys' scores on the attitude toward success scale be viewed as negative? If so, is there evidence to suggest that they are being subjected to forces that undermine their affective dispositions on this component?
These questions are posited as possible foundations for future investigation. Furthermore, they suggest that for a better understanding of the causes of the different affective profiles amongst various sub-groups, there is a need to focus on factors contained within the wider socio-political domain that envelop the members of those sub-groups. When investigations into gender and mathematics are expanded to include these factors, the level of complexity magnifies considerably. Every individual is constrained by cultural norms and values associated with gender; thus, it is these norms and values that have to become part of the investigation. No affective component, as it pertains to any sub-group, can be viewed in isolation.
In Summary.
It has to be accepted that affect is only one element of a complex environment which impacts upon gender differences; however, in attempting to combat the forces that result in a differential and discriminatory environment for girls, it is important to understand the multiple nature of any would-be solutions. Each environmental and learner-related variable that mediates differential experiences for girls has to be identified, understood, and acted upon.
This investigation has attempted to measure affective variables as they relate to the learning of mathematics. An attempt has been made to discern differences between girls' affective scores based upon educational environment, single-sex and co-educational. Most importantly, an understanding of any wider implications that such scores have for the students involved has been sought. The limitations of this study, however, are acknowledged, and the interpretations of the results have to be viewed cautiously.
The results seem to indicate that the single-sex environment utilized in this study may have a positive impact upon the girls' affective profile scores; however, there may also be evidence that, like their co-educated contemporaries, they continue to be constrained by the cultural norms and values associated with gender.
The conclusions that stem from this investigation give rise to several areas upon which the focus of further research is required if we are to address the needs of female students in their study of mathematics. This research should pertain to the investigation of the more positive affective profiles of the single-sex educated girls, as this may lead to gainful insights into appropriate pedagogical approaches. Such analysis affirms girls as central to their own mathematical development, not as somehow deficient. Additionally, investigation needs to be carried out into the social practices that envelop students as gendered learners and the ways in which these impact upon them in the classroom. Study from within such a socially critical framework may equip mathematics educators with a wider range of positions from which to enhance learning.
Without further research, the significance of the results of this investigation are limited; however, the findings have already initiated debate amongst the teachers of mathematics in Bermuda. This is encouraging, as it is through insights into what is happening within our own classrooms that we can attempt to enhance the learning of our students.
As teachers of mathematics, we must ensure that opportunities occur for all students to challenge the rules of mathematics, irrespective of the gender composition of the classroom. Those of us in co-educational classrooms must be particularly aware that such an environment may constrain girls unless we take steps to alleviate this situation. Alternatively, it could be argued that the provision of single-sex classrooms is appropriate, although the data presented here cannot be viewed as conclusive. The degree to which we are successful, however, may well be restricted by forces external to the classroom over which we have little control. Thus, both approaches may be missing the real issue because they attempt only to improve the lot of girls within a society which is otherwise left unchanged. In this way, they may just help to maintain the status quo.
Perhaps, therefore, it is time to consider a more radical approach in which gender issues in the wider community are explicitly confronted in the mathematics classroom. The inclusion of these issues within an expanded mathematics curriculum would help to humanize the subject and allow for wider ownership. Such a curriculum would help students understand how their attitudes concerning mathematics are socially constructed. This, as Willis (1995) states,
. . . would enable both girls and boys to understand how they are positioned differently with respect to mathematics, to identify the processes by which gendered patterns of achievement and participation in mathematics are produced and naturalized, and to recognize the effect of these processes on their futures.
Willis (1995, page 198).
Through such understanding, these students may become empowered to act upon their own positions and those of others in an attempt to combat the forces of inequality.
STUDENT QUESTIONNAIRE.
To the student:
On the following 3 pages there are 50 questions concerning your beliefs about mathematics.
Your answers to these questions will become part of a research project for the University of Exeter in the United Kingdom.
Please be as honest as possible when you answer the questions. There is no need to put your name on the paper and your answers will be kept completely confidential.
PLEASE TICK ONE BOX FOR EACH STATEMENT. |
|||||
Strongly |
Disagree |
Undecided |
Agree |
Strongly |
|
Disagree |
Agree |
||||
| 1. Generally I have felt secure about attempting mathematics. | |||||
| 2. I expect
to have little use for mathematics when I get out of school. |
|||||
| 3. It would
make me happy to be recognised as an excellent student in mathematics. |
|||||
| 4. I would
expect a woman mathematician to be a masculine type of person. |
|||||
| 5. I'll need mathematics for my future work. | |||||
| 6. Math has been my worst subject. | |||||
| 7. Females are as good as males in mathematics. | |||||
| 8. I don't like people to think I'm smart in math. | |||||
| 9. I am sure I could do advanced work in mathematics. | |||||
| 10. In terms
of my adult life it is not important for me to do well in mathematics. |
|||||
| 11. I'd be proud to be the outstanding student in math. | |||||
| 12. Mathematics is for men, arithmetic is for women. | |||||
| 13. I study mathematics because I know how useful it is. | |||||
| 14. Most
subjects I can handle O.K., but I have a knack for messing up in math. |
|||||
| 15. Studying
mathematics is just as appropriate for women as for men. |
|||||
| 16. It would
make people like me less if I were a really good math student. |
|||||
| 17. I am sure that I can learn mathematics. | |||||
| 18. Taking mathematics is a waste of time. | |||||
| 19. I'd be happy to get top grades in mathematics. | |||||
| 20. Girls who enjoy studying math are a bit peculiar. |
|
Strongly |
Disagree |
Undecided |
Agree |
Strongly |
Disagree |
Agree |
||||
| 21. Knowing mathematics will help me earn a living. | |||||
| 22. For some
reason even though I study, math seems unusually hard for me. |
|||||
| 23. I would
trust a woman just as much as I would trust a man to figure out important calculations. |
|||||
| 24. If I got the highest grade in math I'd prefer no one knew. | |||||
| 25. I think I could handle more difficult mathematics. | |||||
| 26. I see
mathematics as a subject I will rarely use in my daily life as an adult. |
|||||
| 27. It would be really great to win a prize in mathematics. | |||||
| 28. I would
have more faith in the answer for a math problem solved by a man than a womam. |
|||||
| 29. Mathematics is a worthwhile and necessary subject. | |||||
| 30. I'm not the type to do well in math. | |||||
| 31. Girls can do just as well as boys in mathematics. | |||||
| 32. If I got the highest grade in math, I would try to hide it. | |||||
| 33. I can get good grades in mathematics. | |||||
| 34. Mathematics will not be important to me in my life's work. | |||||
| 35. Being first in a mathematics competition would make me pleased. | |||||
| 36. When a
woman has to solve a math problem, it is feminine to ask a man for help. |
|||||
| 37. I'll need a firm mastery of mathematics for my future work. | |||||
| 38. I don't think I could do advanced mathematics. | |||||
| 39. Males are not naturally better than females in mathematics. | |||||
| 40. People
would think that I was some kind of creep if I got A's in math. |
|||||
| 41. I have a
lot of self-confidence when it comes to mathematics. |
|||||
| 42. Mathematics is of no relevance to my life. | |||||
| 43. Being
regarded as smart in mathematics would be a great thing. |
|||||
| 44. It's hard
to believe a female could be a genius in mathematics. |
|||||
| 45. I will use mathematics in many ways as an adult. | |||||
| 46. I'm no good in math. | |||||
| 47. Women
certainly are logical enough to do well in mathematics. |
|||||
| 48. Winning a
prize in mathematics would make me feel unpleasantly conspicuous. |
In the following statements, tick the explanation which is most important for you.
Tick only ONE box for each statement.
49. If I do well in maths it is usually because: &127; I am naturally good at it. &127; I work very hard. &127; I was lucky. &127; The work is very easy.
50. If I do badly in maths it is usually because: &127; I am not naturally good at it. &127; I did not work hard enough. &127; I was unlucky. &127; The work is too hard.
Thank you for your help!
Appendix 2: Fennema-Sherman Mathematics Attitude Scales.
Confidence in Learning Mathematics Scale (C).
Weight
1. + Generally I have felt secure about attempting mathematics.
2. + I am sure I could do advanced work in mathematics.
3. + I am sure that I can learn mathematics.
4. + I think I could handle more difficult mathematics.
5. + I can get good grades in mathematics.
6. + I have a lot of self-confidence when it comes to mathematics.
7. - I'm no good in math.
8. - I don't think I could do advanced mathematics.
9. - I'm not the type to do well in math.
10 - For some reason even though I study, math seems unusually hard for me.
11. - Most subjects I can handle O.K., but I have a knack for messing up math.
12. - Math has been my worst subject.
________________________________________________________________
Attitude Toward Success in Mathematics Scale (AS).
Weight
1. + It would make me happy to be recognised as an excellent student in mathematics.
2. + I'd be proud to be the outstanding student in math.
3. + I'd be happy to get top grades in mathematics.
4. + It would be really great to win a prize in mathematics.
5. + Being first in a mathematics competition would make me pleased.
6. + Being regarded as smart in mathematics would be a great thing.
7. - Winning a prize in mathematics would make me feel unpleasantly conspicuous.
8. - People would think that I was some kind of creep if I got A's in math.
9. - If I got the highest grade in math, I would try to hide it.
10. - If I got the highest grade in math I'd prefer no one knew.
11. - It would make people like me less if I were a really good math student.
12. - I don't like people to think I'm smart in math.
Mathematics as a Male Domain Scale (MD).
Weight
1. + Females are as good as males in mathematics.
2. + Studying mathematics is just as appropriate for women as for men.
3. + I would trust a woman just as much as I would trust a man to figure out important calculations.
4. + Girls can do just as well as boys in mathematics.
5. + Males are not naturally better than females in mathematics.
6. + Women certainly are logical enough to do well in mathematics.
7. - It's hard to believe a female could be a genius in mathematics.
8. - When a woman has to solve a math problem, it is feminine to ask a man for help.
9. - I would have more faith in the answer for a math problem solved by a man than a woman.
10. - Girls who enjoy studying math are a bit peculiar.
11. - Mathematics is for men, arithmetic is for women.
12. - I would expect a woman mathematician to be a masculine type of person.
---------------------------------------------------------------------------------------------------------
Usefulness of Mathematics Scale (U).
Weight
1. + I'll need mathematics for my future work.
2. + I study mathematics because I know how useful it is.
3. + Knowing mathematics will help me earn a living.
4. + Mathematics is a worthwhile and necessary subject.
5. + I'll need a firm mastery of mathematics for my future work.
6. + I will use mathematics in many ways as an adult.
7. - Mathematics is of no relevance to my life.
8. - Mathematics will not be important to me in my life's work.
9. - I see mathematics as a subject I will rarely use in my daily life as an adult.
10. - Taking mathematics is a waste of time.
11. - In terms of my adult life it is not important for me to do well in mathematics in high school.
12. - I expect to have little use for mathematics when I get out of school.
Source: Fennema and Sherman (1976, pages 21-27).
Appendix3: Results
3(i): Raw Data.
SS2 |
||||||
n |
C |
U |
AS |
MD |
Attribution |
TOTAL |
1 |
51 |
59 |
60 |
60 |
6 |
236 |
2 |
53 |
56 |
60 |
60 |
6 |
235 |
3 |
51 |
56 |
57 |
60 |
7 |
231 |
4 |
51 |
55 |
58 |
60 |
6 |
230 |
5 |
55 |
58 |
58 |
51 |
7 |
229 |
6 |
58 |
47 |
56 |
60 |
7 |
228 |
7 |
54 |
50 |
59 |
57 |
6 |
226 |
8 |
48 |
58 |
56 |
55 |
7 |
224 |
9 |
58 |
48 |
54 |
55 |
7 |
222 |
10 |
52 |
49 |
50 |
60 |
8 |
219 |
11 |
45 |
57 |
52 |
58 |
6 |
218 |
12 |
50 |
55 |
51 |
54 |
6 |
216 |
13 |
42 |
58 |
53 |
57 |
5 |
215 |
14 |
44 |
55 |
51 |
57 |
7 |
214 |
15 |
38 |
51 |
60 |
60 |
4 |
213 |
16 |
52 |
40 |
57 |
58 |
6 |
213 |
17 |
51 |
50 |
47 |
58 |
7 |
213 |
18 |
51 |
52 |
44 |
58 |
6 |
211 |
19 |
36 |
46 |
60 |
60 |
6 |
208 |
20 |
45 |
42 |
52 |
60 |
5 |
204 |
21 |
35 |
55 |
55 |
51 |
6 |
202 |
22 |
38 |
45 |
50 |
60 |
6 |
199 |
23 |
47 |
43 |
42 |
60 |
6 |
198 |
24 |
37 |
46 |
53 |
56 |
6 |
198 |
25 |
45 |
48 |
52 |
47 |
6 |
198 |
26 |
36 |
55 |
53 |
48 |
6 |
198 |
27 |
48 |
44 |
48 |
51 |
7 |
198 |
28 |
37 |
49 |
51 |
53 |
6 |
196 |
29 |
40 |
45 |
46 |
57 |
6 |
194 |
30 |
40 |
37 |
51 |
60 |
6 |
194 |
31 |
37 |
47 |
49 |
54 |
6 |
193 |
32 |
42 |
41 |
46 |
56 |
7 |
192 |
33 |
24 |
52 |
52 |
58 |
5 |
191 |
34 |
43 |
48 |
37 |
56 |
6 |
190 |
35 |
31 |
50 |
54 |
46 |
6 |
187 |
36 |
45 |
35 |
46 |
53 |
6 |
185 |
37 |
45 |
38 |
37 |
59 |
6 |
185 |
38 |
26 |
38 |
58 |
55 |
6 |
183 |
39 |
38 |
27 |
53 |
57 |
6 |
181 |
40 |
35 |
42 |
39 |
56 |
6 |
178 |
41 |
35 |
35 |
50 |
49 |
6 |
175 |
42 |
36 |
34 |
47 |
50 |
6 |
173 |
43 |
29 |
47 |
39 |
50 |
5 |
170 |
44 |
30 |
32 |
47 |
54 |
6 |
169 |
45 |
27 |
33 |
49 |
53 |
6 |
168 |
46 |
37 |
30 |
48 |
44 |
6 |
165 |
47 |
27 |
45 |
36 |
50 |
6 |
164 |
48 |
32 |
34 |
37 |
54 |
5 |
162 |
49 |
24 |
38 |
50 |
39 |
5 |
156 |
CE2G |
||||||
n |
C |
U |
AS |
MD |
Attribution |
TOTAL |
1 |
54 |
56 |
60 |
55 |
8 |
233 |
2 |
51 |
56 |
56 |
58 |
6 |
227 |
3 |
47 |
55 |
56 |
56 |
6 |
220 |
4 |
46 |
56 |
53 |
56 |
6 |
217 |
5 |
49 |
46 |
56 |
59 |
7 |
217 |
6 |
45 |
57 |
49 |
58 |
7 |
216 |
7 |
35 |
56 |
56 |
60 |
6 |
213 |
8 |
46 |
53 |
51 |
53 |
5 |
208 |
9 |
46 |
50 |
54 |
51 |
6 |
207 |
10 |
40 |
51 |
52 |
56 |
7 |
206 |
11 |
29 |
56 |
54 |
58 |
6 |
203 |
12 |
39 |
46 |
53 |
59 |
6 |
203 |
13 |
46 |
53 |
46 |
50 |
6 |
201 |
14 |
32 |
53 |
52 |
52 |
6 |
195 |
15 |
41 |
49 |
47 |
50 |
7 |
194 |
16 |
32 |
47 |
54 |
54 |
6 |
193 |
17 |
45 |
46 |
49 |
46 |
6 |
192 |
18 |
35 |
44 |
50 |
56 |
6 |
191 |
19 |
33 |
47 |
50 |
53 |
6 |
189 |
20 |
36 |
45 |
48 |
54 |
6 |
189 |
21 |
40 |
37 |
46 |
57 |
6 |
186 |
22 |
33 |
42 |
46 |
59 |
6 |
186 |
23 |
35 |
48 |
47 |
47 |
6 |
183 |
24 |
34 |
45 |
44 |
54 |
4 |
181 |
25 |
41 |
44 |
44 |
45 |
5 |
179 |
26 |
32 |
48 |
43 |
48 |
6 |
177 |
27 |
34 |
23 |
53 |
59 |
6 |
175 |
28 |
32 |
43 |
45 |
44 |
6 |
170 |
29 |
27 |
40 |
46 |
52 |
4 |
169 |
30 |
32 |
39 |
45 |
47 |
5 |
168 |
31 |
27 |
33 |
43 |
59 |
6 |
168 |
32 |
29 |
41 |
37 |
49 |
5 |
161 |
33 |
32 |
46 |
35 |
41 |
6 |
160 |
34 |
21 |
39 |
48 |
40 |
4 |
152 |
35 |
25 |
28 |
34 |
33 |
5 |
125 |
SS5 |
||||||
n |
C |
U |
AS |
MD |
Attribution |
TOTAL |
1 |
59 |
58 |
56 |
59 |
7 |
239 |
2 |
56 |
57 |
58 |
60 |
6 |
237 |
3 |
56 |
58 |
56 |
60 |
6 |
236 |
4 |
60 |
57 |
53 |
57 |
7 |
234 |
5 |
55 |
52 |
56 |
60 |
6 |
229 |
6 |
53 |
58 |
53 |
57 |
6 |
227 |
7 |
49 |
53 |
60 |
58 |
6 |
226 |
8 |
52 |
50 |
57 |
60 |
6 |
225 |
9 |
52 |
56 |
50 |
60 |
7 |
225 |
10 |
52 |
48 |
54 |
57 |
7 |
218 |
11 |
47 |
58 |
50 |
53 |
6 |
214 |
12 |
47 |
56 |
51 |
52 |
6 |
212 |
13 |
41 |
57 |
51 |
57 |
6 |
212 |
14 |
53 |
53 |
44 |
55 |
7 |
212 |
15 |
41 |
49 |
54 |
60 |
6 |
210 |
16 |
50 |
46 |
51 |
57 |
6 |
210 |
17 |
56 |
48 |
47 |
53 |
6 |
210 |
18 |
46 |
49 |
53 |
53 |
6 |
207 |
19 |
51 |
47 |
53 |
49 |
6 |
206 |
20 |
47 |
49 |
52 |
50 |
7 |
205 |
21 |
37 |
47 |
56 |
57 |
6 |
203 |
22 |
42 |
43 |
56 |
55 |
6 |
202 |
23 |
40 |
44 |
55 |
56 |
6 |
201 |
24 |
46 |
36 |
52 |
60 |
6 |
200 |
25 |
53 |
43 |
46 |
51 |
7 |
200 |
26 |
29 |
45 |
59 |
60 |
6 |
199 |
27 |
27 |
49 |
59 |
58 |
6 |
199 |
28 |
41 |
37 |
54 |
60 |
6 |
198 |
29 |
35 |
44 |
58 |
55 |
6 |
198 |
30 |
41 |
53 |
47 |
50 |
6 |
197 |
31 |
43 |
36 |
50 |
51 |
6 |
186 |
32 |
36 |
49 |
48 |
46 |
6 |
185 |
33 |
38 |
43 |
44 |
54 |
4 |
183 |
34 |
42 |
46 |
48 |
41 |
6 |
183 |
35 |
47 |
40 |
44 |
44 |
6 |
181 |
36 |
24 |
40 |
54 |
53 |
4 |
175 |
37 |
28 |
42 |
45 |
52 |
5 |
172 |
38 |
32 |
35 |
52 |
47 |
5 |
171 |
39 |
26 |
41 |
45 |
51 |
5 |
168 |
40 |
25 |
31 |
43 |
53 |
6 |
158 |
CE5G |
||||||
n |
C |
U |
AS |
MD |
Attribution |
TOTAL |
1 |
56 |
55 |
60 |
60 |
6 |
237 |
2 |
48 |
58 |
58 |
60 |
7 |
231 |
3 |
50 |
57 |
58 |
55 |
6 |
226 |
4 |
42 |
52 |
56 |
56 |
6 |
212 |
5 |
43 |
45 |
58 |
56 |
6 |
208 |
6 |
45 |
45 |
54 |
58 |
6 |
208 |
7 |
44 |
48 |
49 |
60 |
7 |
208 |
8 |
53 |
41 |
51 |
56 |
7 |
208 |
9 |
51 |
45 |
47 |
58 |
6 |
207 |
10 |
44 |
47 |
55 |
53 |
6 |
205 |
11 |
41 |
46 |
59 |
49 |
6 |
201 |
12 |
38 |
54 |
56 |
45 |
6 |
199 |
13 |
40 |
39 |
51 |
60 |
6 |
196 |
14 |
39 |
46 |
50 |
53 |
6 |
194 |
15 |
43 |
38 |
52 |
52 |
6 |
191 |
16 |
34 |
51 |
46 |
49 |
6 |
186 |
17 |
37 |
46 |
47 |
50 |
6 |
186 |
18 |
34 |
51 |
48 |
47 |
6 |
186 |
19 |
37 |
45 |
49 |
49 |
5 |
185 |
20 |
36 |
46 |
47 |
50 |
6 |
185 |
21 |
35 |
40 |
50 |
52 |
6 |
183 |
22 |
27 |
46 |
49 |
49 |
6 |
177 |
23 |
31 |
38 |
52 |
50 |
6 |
177 |
24 |
30 |
49 |
45 |
47 |
5 |
176 |
25 |
29 |
41 |
54 |
47 |
4 |
175 |
26 |
35 |
38 |
47 |
46 |
6 |
172 |
27 |
33 |
40 |
44 |
48 |
6 |
171 |
28 |
38 |
41 |
39 |
47 |
4 |
169 |
29 |
27 |
41 |
47 |
47 |
6 |
168 |
30 |
22 |
38 |
51 |
50 |
4 |
165 |
31 |
26 |
36 |
42 |
46 |
5 |
155 |
CE2B |
||||||
n |
C |
U |
AS |
MD |
Attribution |
TOTAL |
1 |
60 |
56 |
52 |
60 |
7 |
235 |
2 |
54 |
52 |
60 |
60 |
7 |
233 |
3 |
49 |
59 |
56 |
56 |
6 |
226 |
4 |
56 |
55 |
50 |
48 |
7 |
216 |
5 |
49 |
55 |
51 |
54 |
6 |
215 |
6 |
50 |
56 |
53 |
48 |
6 |
213 |
7 |
51 |
53 |
47 |
47 |
7 |
205 |
8 |
37 |
53 |
49 |
57 |
7 |
203 |
9 |
52 |
44 |
46 |
50 |
7 |
199 |
10 |
48 |
50 |
46 |
47 |
6 |
197 |
11 |
48 |
40 |
48 |
54 |
6 |
196 |
12 |
55 |
47 |
44 |
43 |
7 |
196 |
13 |
29 |
56 |
52 |
51 |
6 |
194 |
14 |
45 |
49 |
43 |
48 |
6 |
191 |
15 |
42 |
47 |
45 |
44 |
7 |
185 |
16 |
40 |
45 |
47 |
45 |
5 |
182 |
17 |
35 |
46 |
48 |
45 |
6 |
180 |
18 |
43 |
44 |
41 |
45 |
7 |
180 |
19 |
28 |
41 |
47 |
54 |
6 |
176 |
20 |
31 |
41 |
51 |
41 |
7 |
171 |
21 |
32 |
39 |
32 |
59 |
6 |
168 |
22 |
34 |
35 |
40 |
37 |
6 |
152 |
23 |
42 |
26 |
38 |
37 |
7 |
150 |
24 |
35 |
32 |
34 |
41 |
5 |
147 |
25 |
22 |
33 |
45 |
42 |
5 |
147 |
CE5B |
||||||
n |
C |
U |
AS |
MD |
Attribution |
TOTAL |
1 |
59 |
59 |
58 |
59 |
7 |
242 |
2 |
55 |
58 |
59 |
53 |
8 |
233 |
3 |
57 |
48 |
59 |
60 |
7 |
231 |
4 |
60 |
55 |
59 |
50 |
6 |
230 |
5 |
54 |
58 |
57 |
55 |
6 |
230 |
6 |
60 |
59 |
53 |
43 |
7 |
222 |
7 |
55 |
55 |
53 |
52 |
6 |
221 |
8 |
37 |
56 |
59 |
60 |
6 |
218 |
9 |
48 |
47 |
59 |
48 |
6 |
208 |
10 |
46 |
55 |
49 |
52 |
6 |
208 |
11 |
52 |
51 |
53 |
42 |
6 |
204 |
12 |
41 |
45 |
57 |
55 |
6 |
204 |
13 |
47 |
50 |
48 |
47 |
6 |
198 |
14 |
42 |
50 |
47 |
52 |
6 |
197 |
15 |
35 |
58 |
42 |
56 |
6 |
197 |
16 |
44 |
45 |
52 |
49 |
5 |
195 |
17 |
42 |
51 |
48 |
46 |
6 |
193 |
18 |
32 |
41 |
55 |
52 |
6 |
186 |
19 |
29 |
37 |
56 |
54 |
6 |
182 |
20 |
42 |
46 |
34 |
38 |
5 |
165 |
21 |
40 |
42 |
40 |
36 |
6 |
164 |
22 |
37 |
37 |
37 |
36 |
6 |
153 |
Appendix 3(ii): Analysis of the degree of linear relationship between student
attribution scores and their total* scores for confidence (C), usefulness (U), attitude to success (AS) and mathematics as a male domain (MD) scales using Pearson's Product Moment Correlation Coefficient (r).
SS2 |
SS2 (cont.) | |||||||
n |
Total* (X) |
Attribution (Y) |
n |
Total* (X) |
Attribution (Y) |
|||
1 |
230 |
6 |
26 |
192 |
6 |
|||
2 |
229 |
6 |
27 |
191 |
7 |
|||
3 |
224 |
7 |
28 |
190 |
6 |
|||
4 |
224 |
6 |
29 |
188 |
6 |
|||
5 |
222 |
7 |
30 |
188 |
6 |
|||
6 |
221 |
7 |
31 |
187 |
6 |
|||
7 |
220 |
6 |
32 |
186 |
5 |
|||
8 |
217 |
7 |
33 |
185 |
7 |
|||
9 |
215 |
7 |
34 |
184 |
6 |
|||
10 |
212 |
6 |
35 |
181 |
6 |
|||
11 |
211 |
8 |
36 |
179 |
6 |
|||
12 |
210 |
5 |
37 |
179 |
6 |
|||
13 |
210 |
6 |
38 |
177 |
6 |
|||
14 |
209 |
4 |
39 |
175 |
6 |
|||
15 |
207 |
7 |
40 |
172 |
6 |
|||
16 |
207 |
6 |
41 |
169 |
6 |
|||
17 |
206 |
7 |
42 |
167 |
6 |
|||
18 |
205 |
6 |
43 |
165 |
5 |
|||
19 |
202 |
6 |
44 |
163 |
6 |
|||
20 |
199 |
5 |
45 |
162 |
6 |
|||
21 |
196 |
6 |
46 |
159 |
6 |
|||
22 |
193 |
6 |
47 |
158 |
6 |
|||
23 |
192 |
6 |
48 |
157 |
5 |
|||
24 |
192 |
6 |
49 |
151 |
5 |
|||
25 |
192 |
6 |
||||||
| n = 49 | ||||||||
� |
X = 9450 | r = |
n� CU - (�C)(�U) | |||||
� |
Y = 297 | � [( n�C2 - (�C)2 )( n�U2 - (�U)2] | ||||||
� |
XY = 57524 | |||||||
� |
X� = 1844042 | r = |
0.35 | (Significant at 1%) | ||||
� |
Y� = 1823 | |||||||
( � |
X)� = 89302500 | |||||||
( � |
Y)� = 88209 | |||||||
CE2G |
|||||||
n |
Total* (X) |
Attribution(Y) |
|||||
1 |
225 |
8 |
|||||
2 |
221 |
6 |
|||||
3 |
214 |
6 |
n = 35 | ||||
4 |
211 |
6 |
� |
X = 6449 | |||
5 |
210 |
7 |
� |
Y = 205 | |||
6 |
209 |
7 |
� |
XY = 38153 | |||
7 |
207 |
6 |
� |
X� = 1205551 | |||
8 |
203 |
5 |
� |
Y� = 1225 | |||
9 |
201 |
6 |
(� |
X)� = 41589601 | |||
10 |
199 |
7 |
(� |
Y)� = 42025 | |||
11 |
197 |
6 |
|||||
12 |
197 |
6 |
|||||
13 |
195 |
6 |
|||||
14 |
189 |
6 |
|||||
15 |
187 |
7 |
r = |
n�CU - (�C)(�U) | |||
16 |
187 |
6 |
� [( n�C2 - (�C)2)( n�U2 - (�U)2)] | ||||
17 |
186 |
6 |
|||||
18 |
185 |
6 |
r = |
0.587 | (Significant at 0.05%) | ||
19 |
183 |
6 |
|||||
20 |
183 |
6 |
|||||
21 |
180 |
6 |
|||||
22 |
180 |
6 |
|||||
23 |
177 |
4 |
|||||
24 |
177 |
6 |
|||||
25 |
174 |
5 |
|||||
26 |
171 |
6 |
|||||
27 |
169 |
6 |
|||||
28 |
165 |
4 |
|||||
29 |
164 |
6 |
|||||
30 |
163 |
5 |
|||||
31 |
162 |
6 |
|||||
32 |
156 |
5 |
|||||
33 |
154 |
6 |
|||||
34 |
148 |
4 |
|||||
35 |
120 |
5 |
|||||
SS5 |
|||||||
n |
Total* (X) |
Attribution (Y) |
|||||
1 |
230 |
7 |
|||||
2 |
229 |
6 |
|||||
3 |
228 |
6 |
n = 40 | ||||
4 |
225 |
7 |
� |
X = 7831 | |||
5 |
221 |
6 |
� |
Y = 240 | |||
6 |
219 |
6 |
� |
XY = 47276 | |||
7 |
218 |
6 |
� |
X� = 1548709 | |||
8 |
217 |
6 |
� |
Y� = 1458 | |||
9 |
216 |
7 |
(� |
X)� = 61324561 | |||
10 |
209 |
7 |
(� |
Y)� = 57600 | |||
11 |
206 |
6 |
|||||
12 |
204 |
6 |
|||||
13 |
204 |
6 |
|||||
14 |
203 |
7 |
|||||
15 |
202 |
6 |
r = |
n�CU - (�C)(�U) | |||
16 |
202 |
6 |
� [( n�C2 - (�C)2)( n�U2 - (�U)2)] | ||||
17 |
202 |
6 |
|||||
18 |
199 |
6 |
r = |
0.547 | (Significant at 0.05%) | ||
19 |
198 |
6 |
|||||
20 |
196 |
7 |
|||||
21 |
195 |
6 |
|||||
22 |
194 |
6 |
|||||
23 |
193 |
6 |
|||||
24 |
192 |
6 |
|||||
25 |
191 |
6 |
|||||
26 |
191 |
6 |
|||||
27 |
191 |
7 |
|||||
28 |
190 |
6 |
|||||
29 |
190 |
6 |
|||||
30 |
189 |
6 |
|||||
31 |
178 |
6 |
|||||
32 |
177 |
4 |
|||||
33 |
177 |
6 |
|||||
34 |
175 |
6 |
|||||
35 |
173 |
6 |
|||||
36 |
169 |
4 |
|||||
37 |
165 |
5 |
|||||
38 |
164 |
5 |
|||||
39 |
159 |
5 |
|||||
40 |
150 |
6 |
|||||
CE5G |
|||||||
n |
Total* (X) |
Attribution (Y) |
|||||
1 |
231 |
6 |
|||||
2 |
224 |
7 |
|||||
3 |
220 |
6 |
n = 31 | ||||
4 |
206 |
6 |
� |
X = 5767 | |||
5 |
202 |
6 |
� |
Y = 180 | |||
6 |
202 |
6 |
� |
XY = 32485 | |||
7 |
201 |
7 |
� |
X� = 1084333 | |||
8 |
201 |
6 |
� |
Y� = 1062 | |||
9 |
201 |
7 |
(� |
X)� = 33258289 | |||
10 |
199 |
6 |
(� |
Y)� = 32400 | |||
11 |
195 |
6 |
|||||
12 |
193 |
6 |
|||||
13 |
190 |
6 |
|||||
14 |
188 |
6 |
|||||
15 |
185 |
6 |
r = |
n�CU - (�C)(�U) | |||
16 |
180 |
6 |
� [( n�C2 - (�C)2)( n�U2 - (�U)2)] | ||||
17 |
180 |
6 |
|||||
18 |
180 |
6 |
r = |
0.562 | (Significant at 0.05%) | ||
19 |
180 |
5 |
|||||
20 |
179 |
6 |
|||||
21 |
177 |
6 |
|||||
22 |
171 |
4 |
|||||
23 |
171 |
5 |
|||||
24 |
171 |
6 |
|||||
25 |
171 |
6 |
|||||
26 |
166 |
6 |
|||||
27 |
165 |
4 |
|||||
28 |
165 |
6 |
|||||
29 |
162 |
6 |
|||||
30 |
161 |
4 |
|||||
31 |
150 |
5 |
|||||
CE2B |
|||||||
n |
Total* (X) |
Attribution (Y) |
|||||
1 |
228 |
7 |
|||||
2 |
226 |
7 |
|||||
3 |
220 |
6 |
n = 25 | ||||
4 |
209 |
7 |
� |
X = 4599 | |||
5 |
209 |
6 |
� |
Y = 158 | |||
6 |
207 |
6 |
� |
XY = 29229 | |||
7 |
198 |
7 |
� |
X� = 861377 | |||
8 |
196 |
7 |
� |
Y� = 1010 | |||
9 |
192 |
7 |
(� |
X)� = 21150801 | |||
10 |
191 |
6 |
(� |
Y)� = 24964 | |||
11 |
190 |
6 |
|||||
12 |
189 |
7 |
|||||
13 |
188 |
6 |
|||||
14 |
185 |
6 |
|||||
15 |
178 |
7 |
r = |
n�CU - (�C)(�U) | |||
16 |
177 |
5 |
� [( n�C2 - (�C)2) ( n�U2 - (�U)2)] | ||||
17 |
174 |
6 |
|||||
18 |
173 |
7 |
r = |
0.39 | (Significant at 5%) | ||
19 |
170 |
6 |
|||||
20 |
164 |
7 |
|||||
21 |
162 |
6 |
|||||
22 |
146 |
6 |
|||||
23 |
143 |
7 |
|||||
24 |
142 |
5 |
|||||
25 |
142 |
5 |
|||||
CE5B |
|||||||
n |
Total* (X) |
Attribution (Y) |
|||||
1 |
235 |
7 |
|||||
2 |
225 |
8 |
|||||
3 |
224 |
7 |
n = 22 | ||||
4 |
224 |
6 |
� |
X = 4346 | |||
5 |
224 |
6 |
� |
Y = 135 | |||
6 |
215 |
6 |
� |
XY = 26850 | |||
7 |
215 |
7 |
� |
X� = 870232 | |||
8 |
212 |
6 |
� |
Y� = 837 | |||
9 |
202 |
6 |
(� |
X)� = 18887716 | |||
10 |
202 |
6 |
(� |
Y)� = 18225 | |||
11 |
198 |
6 |
|||||
12 |
198 |
6 |
|||||
13 |
192 |
6 |
|||||
14 |
191 |
6 |
|||||
15 |
191 |
6 |
r = |
n�CU - (�C)(�U) | |||
16 |
190 |
5 |
� [( n�C2 - (�C)2)( n�U2 - (�U)2)] | ||||
17 |
187 |
6 |
|||||
18 |
180 |
6 |
r = |
0.572 | (Significant at 0.5%) | ||
19 |
176 |
6 |
|||||
20 |
160 |
5 |
|||||
21 |
158 |
6 |
|||||
22 |
147 |
6 |
|||||
Appendix 3(iii): Descriptive Statistics.
SS2 |
C |
U |
AS |
MD |
Attribution |
TOTAL |
| Mean | 41.45 |
46.02 |
50.41 |
54.98 |
6.06 |
198.92 |
| Median | 42 |
47 |
51 |
56 |
6 |
198 |
| Mode | 51 |
55 |
60 |
60 |
6 |
198 |
| Standard Deviation | 9.18 |
8.41 |
6.58 |
4.85 |
0.69 |
21.44 |
| Variance | 84.29 |
70.81 |
43.29 |
23.56 |
0.48 |
459.49 |
| Range | 34 |
32 |
24 |
21 |
4 |
80 |
| Minimum | 24 |
27 |
36 |
39 |
4 |
156 |
| Maximum | 58 |
59 |
60 |
60 |
8 |
236 |
| Sum | 2031 |
2255 |
2470 |
2694 |
297 |
9747 |
| Count | 49 |
49 |
49 |
49 |
49 |
49 |
CE2G |
C |
U |
AS |
MD |
Attribution |
TOTAL |
| Mean | 37.17 |
46.23 |
48.63 |
52.23 |
5.86 |
190.11 |
| Median | 35 |
46 |
49 |
54 |
6 |
191 |
| Mode | 32 |
56 |
56 |
59 |
6 |
217 |
| Standard Deviation | 8 |
8.05 |
6 |
6.39 |
0.85 |
23.05 |
| Variance | 63.97 |
64.83 |
36.01 |
40.77 |
0.71 |
531.22 |
| Range | 33 |
34 |
26 |
27 |
4 |
108 |
| Minimum | 21 |
23 |
34 |
33 |
4 |
125 |
| Maximum | 54 |
57 |
60 |
60 |
8 |
233 |
| Sum | 1301 |
1618 |
1702 |
1828 |
205 |
6654 |
| Count | 35 |
35 |
35 |
35 |
35 |
35 |
SS5 |
C |
U |
AS |
MD |
Attribution |
TOTAL |
| Mean | 43.88 |
47.58 |
51.85 |
54.53 |
6 |
203.83 |
| Median | 46 |
48 |
52.5 |
55 |
6 |
204 |
| Mode | 47 |
49 |
56 |
60 |
6 |
212 |
| Standard Deviation | 10.02 |
7.28 |
4.73 |
4.83 |
0.68 |
20.28 |
| Variance | 100.32 |
53.07 |
22.34 |
23.33 |
0.46 |
411.43 |
| Range | 36 |
27 |
17 |
19 |
3 |
81 |
| Minimum | 24 |
31 |
43 |
41 |
4 |
158 |
| Maximum | 60 |
58 |
60 |
60 |
7 |
239 |
| Sum | 1755 |
1903 |
2074 |
2181 |
240 |
8153 |
| Count | 40 |
40 |
40 |
40 |
40 |
40 |
CE5G |
C |
U |
AS |
MD |
Attribution |
TOTAL |
| Mean | 38.32 |
45.26 |
50.68 |
51.77 |
5.81 |
191.84 |
| Median | 38 |
45 |
50 |
50 |
6 |
186 |
| Mode | 43 |
46 |
47 |
47 |
6 |
208 |
| Standard Deviation | 8.32 |
5.98 |
5.21 |
4.83 |
0.75 |
20 |
| Variance | 69.23 |
35.8 |
27.09 |
23.31 |
0.56 |
399.87 |
| Range | 34 |
22 |
21 |
15 |
3 |
82 |
| Minimum | 22 |
36 |
39 |
45 |
4 |
155 |
| Maximum | 56 |
58 |
60 |
60 |
7 |
237 |
| Sum | 1188 |
1403 |
1571 |
1605 |
180 |
5947 |
| Count | 31 |
31 |
31 |
31 |
31 |
31 |
CE2B |
C |
U |
AS |
MD |
Attribution |
TOTAL |
| Mean | 42.68 |
46.16 |
46.6 |
48.52 |
6.32 |
190.28 |
| Median | 43 |
47 |
47 |
48 |
6 |
194 |
| Mode | 49 |
56 |
47 |
48 |
7 |
196 |
| Standard Deviation | 10.05 |
8.71 |
6.37 |
6.81 |
0.69 |
25.56 |
| Variance | 100.98 |
75.89 |
40.58 |
46.43 |
0.48 |
653.46 |
| Range | 38 |
33 |
28 |
23 |
2 |
88 |
| Minimum | 22 |
26 |
32 |
37 |
5 |
147 |
| Maximum | 60 |
59 |
60 |
60 |
7 |
235 |
| Sum | 1067 |
1154 |
1165 |
1213 |
158 |
4757 |
| Count | 25 |
25 |
25 |
25 |
25 |
25 |
CE5B |
C |
U |
AS |
MD |
Attribution |
TOTAL |
| Mean | 46.09 |
50.14 |
51.55 |
49.77 |
6.14 |
203.68 |
| Median | 45 |
50.5 |
53 |
52 |
6 |
204 |
| Mode | 42 |
58 |
59 |
52 |
6 |
230 |
| Standard Deviation | 9.33 |
7 |
7.6 |
7.19 |
0.64 |
23.97 |
| Variance | 87.13 |
48.98 |
57.78 |
51.71 |
0.41 |
574.8 |
| Range | 31 |
22 |
25 |
24 |
3 |
89 |
| Minimum | 29 |
37 |
34 |
36 |
5 |
153 |
| Maximum | 60 |
59 |
59 |
60 |
8 |
242 |
| Sum | 1014 |
1103 |
1134 |
1095 |
135 |
4481 |
| Count | 22 |
22 |
22 |
22 |
22 |
22 |
| Appendix 3 (iv): z-tests
for hypotheses pertaining to the population means.
z-Test: Two-Sample for Means |
||||||||||||
SS2 vs. CE2G |
C |
C |
U |
U |
AS |
AS |
MD |
MD |
Attribution |
Attribution |
TOTAL |
TOTAL |
| Mean | 41.44 |
37.17 |
46.02 |
46.23 |
50.41 |
48.63 |
54.98 |
52.23 |
6.06 |
5.86 |
198.92 |
190.11 |
| Known Variance | 84.29 |
63.97 |
70.81 |
64.83 |
43.29 |
36.01 |
23.56 |
40.77 |
0.48 |
0.71 |
459.49 |
531.22 |
| Observations | 49 |
35 |
49 |
35 |
49 |
35 |
49 |
35 |
49 |
35 |
49 |
35 |
| Hypothesized Mean Difference | 0 |
0 |
0 |
0 |
0 |
0 |
||||||
| z | 2.271 |
-0.115 |
1.287 |
2.144 |
1.176 |
1.777 |
||||||
| z Critical one-tail | 2.054 |
1.645 |
1.645 |
2.054 |
1.645 |
1.645 |
||||||
| Significance Level | 2% |
Not sig. |
Not sig. |
2% |
Not Sig. |
5% |
||||||
| z-Test: Two-Sample for Means | ||||||||||||
SS5 vs. CE5G |
C |
C |
U |
U |
AS |
AS |
MD |
MD |
Attribution |
Attribution |
TOTAL |
TOTAL |
| Mean | 43.88 |
38.32 |
47.58 |
45.26 |
51.85 |
50.68 |
54.53 |
51.77 |
6 |
5.81 |
203.83 |
191.84 |
| Known Variance | 100.32 |
69.23 |
53.07 |
35.8 |
22.34 |
27.09 |
23.33 |
23.32 |
0.46 |
0.56 |
411.43 |
399.87 |
| Observations | 40 |
31 |
40 |
31 |
40 |
31 |
40 |
31 |
40 |
31 |
40 |
31 |
| Hypothesized Mean Difference | 0 |
0 |
0 |
0 |
0 |
0 |
||||||
| z | 2.55 |
1.471 |
0.98 |
2.38 |
1.124 |
2.489 |
||||||
| z Critical one-tail | 2.326 |
1.645 |
1.645 |
2.326 |
1.645 |
2.326 |
||||||
| Significance Level | 1% |
Not sig. |
Not sig. |
1% |
Not sig. |
1% |
||||||
| z-Test: Two-Sample for Means | ||||||||||||
SS2 vs. CE2B |
C |
C |
U |
U |
AS |
AS |
MD |
MD |
Attribution |
Attribution |
TOTAL |
TOTAL |
| Mean | 41.45 |
42.68 |
46.02 |
46.16 |
50.41 |
46.6 |
54.98 |
48.52 |
6.06 |
6.32 |
198.92 |
190.28 |
| Known Variance | 84.29 |
100.98 |
70.81 |
75.89 |
43.29 |
40.58 |
23.56 |
46.43 |
0.48 |
0.48 |
459.49 |
653.46 |
| Observations | 49 |
25 |
49 |
25 |
49 |
25 |
49 |
25 |
49 |
25 |
49 |
25 |
| Hypothesized Mean Difference | 0 |
0 |
0 |
0 |
0 |
0 |
||||||
| z | -0.513 |
-0.066 |
2.405 |
4.225 |
-1.526 |
1.45 |
||||||
| z Critical two-tail | �1.96 |
�1.96 |
�2.326 |
�2.575 |
�1.96 |
�1.96 |
||||||
| Significance Level | Not Sig. |
Not Sig. |
2% |
1% |
Not Sig. |
Not Sig. |
||||||
| z-Test: Two-Sample for Means | ||||||||||||
SS5 vs. CE5B |
C |
C |
U |
U |
AS |
AS |
MD |
MD |
Attribution |
Attribution |
TOTAL |
TOTAL |
| Mean | 43.88 |
46.09 |
47.58 |
50.14 |
51.85 |
51.55 |
54.53 |
49.77 |
6 |
6.14 |
203.83 |
203.68 |
| Known Variance | 100.32 |
87.13 |
53.07 |
48.98 |
22.34 |
57.78 |
23.33 |
51.71 |
0.46 |
0.41 |
411.43 |
574.8 |
| Observations | 40 |
22 |
40 |
22 |
40 |
22 |
40 |
22 |
40 |
22 |
40 |
22 |
| Hypothesized Mean Difference | 0 |
0 |
0 |
0 |
0 |
0 |
||||||
| z | -0.871 |
-1.359 |
0.171 |
2.775 |
-0.786 |
0.024 |
||||||
| z Critical two-tail | �1.96 |
�1.96 |
�1.96 |
�2.575 |
�1.96 |
�1.96 |
||||||
| Significance Level | Not Sig. |
Not Sig. |
Not Sig. |
1% |
Not Sig. |
Not Sig. |
||||||
| z-Test: Two-Sample for Means | ||||||||||||
CE2G VS. CE2B |
C |
C |
U |
U |
AS |
AS |
MD |
MD |
Attribution |
Attribution |
TOTAL |
TOTAL |
| Mean | 37.17 |
42.68 |
46.23 |
46.16 |
48.63 |
46.6 |
52.23 |
48.52 |
5.86 |
6.32 |
190.11 |
190.28 |
| Known Variance | 63.97 |
100.98 |
46.23 |
75.89 |
36.01 |
40.58 |
40.77 |
51.71 |
0.71 |
0.48 |
513.22 |
653.46 |
| Observations | 35 |
25 |
35 |
25 |
35 |
25 |
35 |
25 |
35 |
25 |
35 |
25 |
| Hypothesized Mean Difference | 0 |
0 |
0 |
0 |
0 |
0 |
||||||
| z | -2.274 |
0.033 |
1.246 |
2.062 |
-2.33 |
-0.026 |
||||||
| z Critical two-tail | �1.96 |
�1.96 |
�1.96 |
�1.96 |
�2.326 |
�1.96 | ||||||
| Significance Level | 5% |
Not Sig. |
Not Sig. |
5% |
2% |
Not Sig. |
||||||
z-Test: Two-Sample for Means |
||||||||||||
CE5G vs CE5B |
C |
C |
U |
U |
AS |
AS |
MD |
MD |
Attribution |
Attribution |
TOTAL |
TOTAL |
| Mean | 38.32 |
46.09 |
45.26 |
50.14 |
50.68 |
51.55 |
51.77 |
49.77 |
5.81 |
6.14 |
186.03 |
203.68 |
| Known Variance | 69.23 |
87.13 |
35.8 |
48.98 |
27.09 |
57.78 |
23.31 |
51.71 |
0.56 |
0.41 |
399.87 |
574.8 |
| Observations | 31 |
22 |
31 |
22 |
31 |
22 |
31 |
22 |
31 |
22 |
31 |
22 |
| Hypothesized Mean Difference | 0 |
0 |
0 |
0 |
0 |
0 |
||||||
| z | -3.121 |
-2.653 |
-0.464 |
1.136 |
-1.722 |
-2.825 |
||||||
| z Critical two-tail | �2.575 |
�2.575 |
�1.96 |
�1.96 |
�1.96 |
�2.575 |
||||||
| Significance Level | 1% |
1% |
Not Sig. |
Not Sig. |
Not Sig. |
1% |
||||||
American Association of University Women (1992) How Schools Shortchange Girls, Washington: American Association of University Women in
conjunction with the National Education Association.
Armstrong, J. M. and Price, R.A. (1982) 'Correlates and Predictors of Women's Mathematics Participation', Journal for Research in Mathematics Education, 13(2), 99-109.
Assessment of Performance Unit (1988), Attitudes and Gender Differences, Windsor: NFER-Nelson.
Badger, E. (1981) Why Aren't Girls Better at Maths?, in Entwhistle, N. (Ed.) (1985) New Directions in Educational Psychology 1. Learning and Teaching, Philadelphia: Falmer, 227-39.
Baker, D. P. and Jones, D. P. (1993) 'Creating Gender Equality: Cross-National Gender Stratification and Mathematical Performance', Sociology of Education, 66(2), 91-103.
Bell-Gredler, M. E. (1986) Learning and Instruction: Theory and Practice, New York: Macmillan.
Benbow, C. and Stanley, J. (1980) 'Sex Differences in Mathematical Ability: Fact or Artifact?', Science, 210, 1262-4.
Blum-Anderson, J. (1989) 'Affect and Mathematics: Persistence in the Mathematical Environment'. Paper presented at the Conference on Women in Mathematics and Sciences. St. Cloud University, Nov. 10-11, 1989.
Bridgeman, B. and Wendler, C. (1990) Prediction of Grades in College Mathematical Courses as a Component of SAT-M Placement Validity, New York: College Entrance Examination Board.
Broadbooks, W. J., Elmore, P. B., Pederson, K. and Bleyer, D. R. (1981) 'A Construct Validation Study of the Fennema-Sherman Mathematics Attitude Scales', Educational and Psychological Measurement, 41(2), 551-57.
Brown, S. (1984) 'The Logic of Problem Generation: From Morality and Solving to De-Posing and Rebellion', For the Learning of Mathematics, 4(1), 9-20.
Burton, L. (Ed.) (1986) Girls Into Maths Can Go, London: Cassell.
Burton, L. (Ed.) (1990) Gender and Mathematics: An International Perspective, London: Cassell.
Burton, L. and Townsend, R. (1985) Girl Friendly Mathematics, in Burton, L. (Ed.) (1986) Girls Into Maths Can Go, London: Cassell, 187-95.
Cairns, E. (1990) 'The Relationship Between Adolescent Perceived Self- Competence and Attendance at Single-Sex Secondary School', British Journal of Educational Psychology, 60(3), 207-211.
Campbell, P. B. (1995) Redefining the "Girl Problem in Mathematics", in Secada, W. G., Fennema, E. and Adajian, L. B. (Eds.) (1995) New Directions for Equity in Mathematics Education, Cambridge: Cambridge University Press, 225-41.
Cockcroft, W. H. (Chair) (1982) Mathematics Counts, London: HMSO.
College Entrance Examination Board and Educational Testing Service (1990) 5 SATs, New York: The College Board.
College Entrance Examination Board and Educational Testing Service (1996), 'SAT 1 Scores Continue Upward Trend; AP Grows', College Board News, Sept. 1996, 1 & 7.
Crawshaw, J. and Chambers, J. (1984) A Concise Course in A-Level Statistics, Cheltenham: Stanley Thornes.
Dale, R. R. (1969) Mixed or Single-Sex School? Vol. I. A Research Study About Pupil-Teacher Relationships. London: Routledge and Keegan Paul.
Dale, R. R. (1971) Mixed or Single-Sex School? Vol. II. Some Social Aspects. London: Routledge and Keegan Paul.
Dale, R. R. (1974) Mixed or Single-Sex School? Vol. III. Attainment, Attitudes and Overview. London: Routledge and Keegan Paul.
Damarin, S. K. (1995) Gender and Mathematics from a Feminist Standpoint, in Secada, W. G., Fennema, E. and Adajian, L. B. (Eds.) (1995) New Directions for Equity in Mathematics Education, Cambridge: Cambridge University Press, 242-57.
Daniels, H. and Anghileri, J. (1995) Secondary Mathematics and Special Educational Needs, London: Cassell.
Delon, F. (1995) The French Experience: The Effects of De-Segregation, in Rogers, P. and Kaiser, G. (Eds.) (1995) Equity in Mathematics Education: Influences of Feminism and Culture, London: Falmer Press, 141-46.
Department of Education and Science (1982-94) Annual Reports of Statistics of Education: Public Examinations CSE/GCE/GCSE, London: HMSO.
Department of Education and Science (1988) Mathematics for Ages 5 to 16, London: HMSO.
Dossey, J. A., Mullis, V. S., Lindquist, M. M. and Chambers, D. L. (1988) The Mathematics Report Card. Are We Measuring Up? Trends and Achievement Based on the 1986 National Assessment, Princeton: Educational Testing Service.
Dunne, M. and Johnston, J. (1994) Research in Gender and Mathematics Education: The Production of Difference, in Ernest, P. (Ed.) (1994) Mathematics Education and Philosophy: An International Perspective, London: Falmer, 221-29.
Eales, A. (1986) Girls and Mathematics at Oadby Beachamp College, in Burton, L. (Ed.) (1986) Girls Into Maths Can Go, London: Cassell, 163-86.
Eccles, J. (1983) Expectancies, Values, and Academic Behaviors, in Spence, J. T. (Ed.) (1983) Achievement and Achievement Motives, San Francisco: Freeman, 75-146.
Eckard, J. S. (1995) 'Correlating Attitudes and College Majors Among Undergraduate Women'. Dissertation abstract. Chadron State College. ERIC Document Reproduction Service No. ED382123.
Egelman, E. et. al. (1981) Letter to the Editor, Science, 212, 116.
Ernest, P. (1991) The Philosophy of Mathematics Education, London: Falmer.
Ernest, P. (1994) Educational Research, Its Philosophy and Purpose. An Introduction to Reseach Methodology and Paradigms, in Radnor, H. A., (Ed.) (1994) Educational Research Monograph Series, 1. Exeter: University of Exeter.
Ernest, P. (1994a) The Nature of Mathematics and Equal Opportunities, Exeter: University of Exeter School of Education.
Ernest, P. (1994b) Psychology of Learning Mathematics, Exeter: University of Exeter School of Education.
Ernest, P. and Bayliss, P. (1995) Mathematics and Special Educational Needs, Exeter: University of Exeter School of Education.
Evans, J. (1994) Quantitative or Qualitative Research Methodologies: Rivalry or Cooperation?, in Ponte J. P. da and Matos, J. F. (Eds.) (1994) Proceedings of the 18th International Conference on the Psychology of Mathematics Education, Lisbon: University of Lisbon, Vol. 2, 320-27.
Fennema, E. (1981) The Sex Factor, in Fennema, E. (Ed.) (1981) Mathematics Education and Research: Implications for the 80s, Alexandria: Association for Supervision and Curriculum Development, 92-105.
Fennema, E. and Sherman, J. (1976) 'Fennema-Sherman Mathematics Attitude Scales: Instruments Designed to Measure Attitudes Towards the Learning of Mathematics by Females and Males'. Unpublished paper. (Available in microfiche format from Educational Testing Service, Princeton, New Jersey 08541).
Fennema, E. and Sherman, J. (1976a) 'Fennema-Sherman Mathematics Attitude Scales: Instruments Designed to Measure Attitudes Towards the Learning of Mathematics by Females and Males', Journal for Research in Mathematics Education, 7, 324-26.
Fennema, E. and Sherman, J. (1977) 'Sex-related Differences in Mathematics Achievement, Spatial Visualization and Affective Factors', American Educational Research Journal, 14, 51-57.
Foon, A. (1988) 'The Relationship Between School Type and Adolescent Self- Esteem, Attribution Styles and Affiliation Needs: Implications for Educational Outcome', British Journal of Educational Psychology, 58, 44- 54.
Friedman, L. (1989) 'Mathematics and the Gender Gap: A Meta-Analysis of Recent Studies of Sex Differences in Mathematical Tasks', Review of Educational Research, 59, 185-213.
Friedman, L. (1995) Assisting Women to Complete Graduate Degrees, in Rogers, P. and Kaiser, G. (Eds.) (1995) Equity in Mathematics Education: Influences of Feminism and Culture, London: Falmer Press, 147-52.
Gwizdala, J. and Steinback, M. (1990) 'High School Females' Mathematics Attitudes: An Interim Report', School Science and Mathematics, 90(3), Mar. 1990.
Hamilton, M. (1985) 'Performance Levels in Science and Other Subjects for Jamaican Adolescents Attending Single-Sex and Co-educational High Schools', Science Education, 69(4), 535-47.
Hanna, G., Kundiger, E. and Larouche, C. (1990) Mathematical Achievement of Grade 12 Girls in Fifteen Countries, in Burton, L. (Ed.) (1990), Gender and Mathematics: An International Perspective, London: Cassell, 87-97.
Hensel, R. A. M. (1989) 'Mathematical Achievement: Equating the Sexes', School Science and Mathematics, 89 (8), 639-653.
Hiddleston, P. (1995) The Contribution of Girls-Only Schools to Mathematics and Science Education in Malawi, in Rogers, P. and Kaiser, G. (Eds.) (1995) Equity in Mathematics Education: Influences of Feminism and Culture, London: Falmer Press, 147-52.
Horner, B. and Sammons, J. (1989) Rolling Loaded Dice: Use of the Scholastic Aptitude Test (SAT) for Higher Education Admissions in New York State, New York: Public Interest Research Group.
Hugill, B. and Narayan, N. (1995) 'School Inspectors Rewrite League Tables', The Observer, 19 Nov. 1995, 3.
Isaacson, Z. (1989) Of Course You Could Be an Engineer, Dear, But Wouldn't You Rather Be a Nurse or Teacher or Secretary? in Ernest, P. (Ed.) (1989) Mathematics Teaching: The State of the Art, London: Falmer, 188- 94.
Jimenez, E. and Lockheed, M. E. (1989) 'Enhancing Girls' Learning Through Single-Sex Education: Evidence and a Policy Conundrum', Educational Evaluation and Policy Analysis, 11(2), 117-42.
Kaiser, G. and Rogers, P. (1995) Introduction: Equity in Mathematics Education, in Rogers, P. and Kaiser, G. (Eds.) (1995) Equity in Mathematics Education: Influences of Feminism and Culture, London: Falmer Press, 1-10.
Kloosterman, P. (1988) 'Self-Confidence and Motivation in Mathematics', Journal of Educational Psychology, 80(3), 345-51.
Koehler, M. S. and Fennema, E. (1982) Women and Mathematics: Is There a
Problem?, in Hill, S. (Ed.) Education in the 80s: Mathematics, Washington: National Association of the United States, 94-107.
Lantz, A. E. and Smith, G. P. (1981) 'Factors Influencing the Choice of Nonrequired Mathematics Courses', Journal of Educational Psychology, 73(6), 825-37.
Leder, G. C. (1990a) Gender Differences in Mathematics: An Overview, in Fennema, E. and Leder, G. C. (Eds.) (1990) Mathematics and Gender, New York: Teachers College Press, 10-26.
Leder, G. C. (1990b) Gender and Classroom Practice, in Burton, L. (Ed.) (1990) Gender and Mathematics: An International Perspective, London: Cassell, 9-19.
Leder, G. C. (1992) Mathematics and Gender: Changing Perspectives, in Grouws, D. A. (Ed.) (1992) Handbook of Research on Mathematics Teaching and Learning, New York: Macmillan, 597-622.
Leder, G. C. (1995) Equity Inside the Mathematics Classroom: Fact or Artifact?, in Secada, W. G., Fennema, E. and Adajian, L. B. (Eds.) (1995) New Directions for Equity in Mathematics Education, Cambridge: Cambridge University Press, 209-24.
Lee, V. E. and Bryk, A. S. (1986) 'Effects of Single-Sex Secondary Schools on Student Achievement and Attitudes', Journal of Educational Psychology, 78(5), 381-395.
Lee, V. E. and Lockheed, M. E. (1990) 'The Effects of Single-Sex Schooling on Achievement and Attitudes in Nigeria', Comparative Education Review, 34(2), May 1990, 209-31.
Lee, V. E. and Marks, H. (1990) 'Sustained Effects of Single-Sex Secondary Schools Experience on Attitudes, Behaviors, and Values in College', Journal of Educational Psychology, 82(3), 578-92.
Lee, V. E., Marks, H. and Byrd, T. (1993) 'Sexism in Single-Sex and
Coeducational Secondary School Classrooms', Sociology of Education, Jul. 1993.
Ma, X. and Kishor, N. (1997) 'Assessing the Relationship Between Attitude Toward Mathematics and Achievement in Mathematics: A Meta-Analysis', Journal for Research in Mathematics Education, 28(1), 26-47.
Maccoby, E. E. (1990) 'Gender and Relationships', American Psychologist, 45 (4), 513-20.
Maccoby, E. E. and Jacklin, C. N. (1974) The Psychology of Sex Differences, Stanford: Stanford University Press.
Mahony, P. (1985) Schools for the Boys? Co-education Reassessed. London: Hutchinson in association with the Explorations in Feminism Collective.
Marjoram, T. (1994) 'Are / Should Boys and Girls Gifted in Mathematics be Taught Together?', Gifted Education International, 9(3), 152-3.
McCormick, T. M. (1994) Creating the Nonsexist Classroom: A Multicultural Approach. New York: Teachers College Press.
McCornack, R. L. and McLeod, M. M. (1988) 'Gender Bias in the Prediction of College Course Performance', Journal of Educational Measurement, 25(4), 321-32.
McLeod, D. B. (1992) Research on Affect in Mathematics Education: A Reconceptualization, in Grouse, D. A. (Ed.) (1992) Handbook of Research on Mathematics Teaching and Learning, New York: Macmillan, 575-96.
Melanchon, J. G., Thompson, B. and Becnel, S. (1994) 'Measurement of Integrity Scores from the Fennema-Sherman Mathematics Attitude Scales: The Attitudes of Public School Teachers', Educational and Psychological Measurement, 4(1), 187-92.
Meyer, M. R. and Koehler, M. S. (1990) Internal Influences on Gender Differences in Mathematics, in Fennema, E. and Leder, G. C. (Eds.) (1990) Mathematics and Gender, New York: Teachers College Press, 60- 95.
Mills, C. J., et. al. (1993) 'Gender Differences in Academically Talented Young Students' Mathematical Reasoning: Patterns Across Age and Subskills', Journal of Educational Psychology, 85(2), 340-46.
Morrow, C and Morrow, J. (1995) Connecting Women with Mathematics, in Rogers, P. and Kaiser, G. (Eds.) (1995) Equity in Mathematics Education: Influences of Feminism and Culture, London: Falmer Press, 13-26.
Mura, M. (1995) Feminism and Strategies for Redressing Gender Imbalance in Mathematics, in Rogers, P. and Kaiser, G. (Eds.) (1995) Equity in Mathematics Education: Influences of Feminism and Culture, London: Falmer Press, 155-62.
National Coalition of Girls Schools (1993) What Every Girl Should Know, Concord: The National Coalition of Girls Schools.
Noddings, N. (1996) 'Equity and Mathematics: Not a Simple Issue', Journal for Research in Mathematics Education, 27(5). 609-15.
Open University (1986) Girls Into Mathematics, Cambridge: Cambridge University Press.
Orenstein, P. (1994) School Girls: Young Women, Self-Esteem, and the Confidence Gap, New York: Anchor.
Orton, A. (1992) Learning Mathematics: Issues, Theory and Classroom Practice, London: Cassell.
Owen, D. (1985) None of the Above: Behind the Myth of Scholastic Aptitude, Boston: Hougton Mifflin.
Owen, D. (1991). Forward, in Robinson, A. and Katzman, J. (1991) The Princeton Review — Cracking the System: The SAT (and PSAT), New York: Villard Books, vii-ix.
Parker, L. H., Rennie, L. J. and Fraser, B. J. (Eds.) (1995) Gender, Science and Mathematics: Shortening the Shadow, Dordrecht: Kluwer Academic Publishers.
Paulos, J. A. (1988) Innumeracy: Mathematical Illiteracy and its Consequences, New York: Hill and Wang.
Pedersen, K., Bleyer, D. R. and Elmore, P. B. (1985) 'Attitudes and Career Interests of Junior High School Mathematics Students: Implications for the Classroom', Arithmetic Teacher, 32(7), 45-49.
Penfold, P. (1991) 'Wanted: Women Scientists', Summit, Spring 1991, 21-23; reprinted in Women, vol. 4, Boca Raton: Social Issues Resources Services, Inc., article no. 41.
Riordan, C. (1985) 'Public and Catholic Schooling: The Effects of Gender Context Policy', American Journal of Education, 5, 518-40.
Royal Society and the Institute of Mathematics and its Applications (1986) Girls and Mathematics, London: The Royal Society.
Russo, N. F. (1984) Sex-Role Stereotyping, Socialization, and Sexism, in Sargent, A. G. (Ed.) (1984) Beyond Sex Roles, St. Paul: West, 150-67.
Sadker, M and Sadker, D. (1994) Failing at Fairness: How America's Schools Cheat Girls, New York: Charles Scribner's Sons.
Seegers, G. and Boekaerts, M. (1993) 'Task Motivation and Mathematics Achievement in Actual Task Situations', Learning and Instruction, 3 (1993), 133-50.
Seegers, G. and Boekaerts, M. (1996) 'Gender-Related Differences in Self- Referenced Cognitions in Relation to Mathematics', Journal for Research in Mathematics Education, 27(2), 215-40.
Sells, L. (1973) High School Mathematics as the Critical Filter in the Job Market, Berkeley: University of California.
Shaw, J. (1995) Education, Gender and Anxiety, London: Taylor and Francis.
Sherman, J. (1982) 'Continuing in Mathematics: A Longitudinal Study of the Attitudes of High School Girls', Psychology of Women Quarterly, 7(2), 132-40.
Shuard, H. S. (1982) Differences in Mathematical Performance Between Girls and Boys, in Cockcroft, W. H. (Chair) (1982) Mathematics Counts, London: HMSO, 273-87.
Shuard, H. S. (1986) The Relative Attainment of Girls and Boys in Mathematics in the Primary Years, in Burton, L. (Ed.) (1986) Girls Into Maths Can Go, London: Cassell, 22-37.
Smith, H. W. (1975) Strategies of Social Research: The Methodological Imagination, Englewood Cliffs: Prentice Hall.
Smith, S. (1986) Separate Tables? An Investigation Into Single-Sex Setting in Mathematics, London: HMSO.
Smithers, A. and Robinson, P. (1995) Co-educational and Single-Sex Schooling. Manchester: Centre for Education and Employment Research, University of Manchester.
Spender, D. (1982) Invisible Women: The Schooling Scandal, London: Writers and Readers.
Tatre, L. A. (1990) Spacial Skills, Gender and Mathematics, in Fennema, E. and Leder, G. C. (Eds.) (1990) Mathematics and Gender, New York: Teachers College Press, 27-59.
Taylor, L. (1990) American Female and Male University Professors' Mathematical Attitudes and Life Histories, in Burton, L. (Ed.) (1990) Gender and Mathematics: An American Perspective, London: Cassell, 47- 59.
Thompson, D. R. (1995) The METRO Achievement Program: Helping Inner-City Girls Excel, in Rogers, P. and Kaiser, G. (Eds.) (1995) Equity in Mathematics Education: Influences of Feminism and Culture, London: Falmer Press, 13-36.
Tobias, S. (1993) Overcoming Math Anxiety, New York: W. W. Norton.
Wainer, H. and Steinberg, L. (1990) Sex Differences in Performance on the Mathematics Section of the Scholastic Aptitude Test: A Bi-directional Validity Study. Princeton, NJ: Educational Testing Service.
Walden, R. and Walkerdine, V. (1986) Characteristics, Views and Relationships in the Classroom, in Burton, L., (Ed.) (1986) Girls Into Maths Can Go, London: Cassell, 122-46.
Walkerdine, V. and the Girls and Mathematics Unit. (1989) Counting Girls Out, London: Virago.
Willis, S. (1989) 'Real Girls Don't Do Maths': Gender and the Construction of Privilege. Geelong: Deakin University.
Willis, S. (1995) Gender Reform through School Mathematics, in Rogers, P. and Kaiser, G., (Eds.) (1995) Equity in Mathematics Education: Influences of Feminism and Culture, London: Falmer Press, 186-99.
Wilt, E. A., Dunbar, S. B. and Hoover, H. D. (1991) 'A Multivariate Perspective on Sex Differences in Achievement and Later Performance Among Adolescents'. Paper presented at the American Educational Research Association. Chicago, Mar. 20, 1991.
Winchel, R., Fenner, D. and Shaver, P. (1974) 'Impact of Co-education on "Fear of Success" Imagery Expressed by Male and Female High School Students', Journal of Educational Psychology, 66, 726-30.